CHUYÊN ĐỀ 2: HOÁN VỊ, TỔ HỢP
A. MỤC TIÊU:
* Bước đầu HS hiểu về chỉnh hợp, hoán vị và tổ hợp
* Vận dụng kiến thức vào một ssó bài toán cụ thể và thực tế
* Tạo hứng thú và nâng cao kỹ năng giải toán cho HS
B. KIẾN THỨC:
I. Chỉnh hợp:
1. Định nghĩa: Cho một tập hợp X gồm n phần tử. Mỗi cách sắp xếp k phần tử của tập hợp X ( 1 k n) theo một thứ tự nhất định gọi là một chỉnh hợp chập k của n phần tử ấy
Số tất cả các chỉnh hợp chập k của n phần tử được kí hiệu $ displaystyle A_{k}^{n}$
2. Tính số chỉnh chập k của n phần tử
II. Hoán vị:
1. Định nghĩa: Cho một tập hợp X gồm n phần tử. Mỗi cách sắp xếp n phần tử của tập hợp X theo một thứ tự nhất định gọi là một hoán vị của n phần tử ấy
Số tất cả các hoán vị của n phần tử được kí hiệu Pn
2. Tính số hoán vị của n phần tử
( n! : n giai thừa)
III. Tổ hợp:
1. Định nghĩa: Cho một tập hợp X gồm n phần tử. Mỗi tập con của X gồm k phần tử trong n phần tử của tập hợp X ( 0 k n) gọi là một tổ hợp chập k của n phần tử ấy
Số tất cả các tổ hợp chập k của n phần tử được kí hiệu $ displaystyle C_{k}^{n}$
2. Tính số tổ hợp chập k của n phần tử
C. Ví dụ:
1. Ví dụ 1:
Cho 5 chữ số: 1, 2, 3, 4, 5
a) có bao nhiêu số tự nhiên có ba chữ số, các chữ số khác nhau, lập bởi ba trong các chữ số trên
b) Có bao nhiêu số tự nhiên có 5 chữ số, các chữ số khác nhau, lập bởi cả 5 chữ số trên
c)Có bao nhiêu cách chọn ra ba chữ số trong 5 chữ số trên
Giải:
a) số tự nhiên có ba chữ số, các chữ số khác nhau, lập bởi ba trong các chữ số trên là chỉnh hợp chập 3 của 5 phần tử: $ displaystyle mathop{text{A}}_{text{5}}^{text{3}}$ = 5.(5 – 1).(5 – 2) = 5 . 4 . 3 = 60 số
b) số tự nhiên có 5 chữ số, các chữ số khác nhau, lập bởi cả 5 chữ số trên là hoán vị cua 5 phần tử (chỉnh hợp chập 5 của 5 phần tử):
$ displaystyle mathop{text{A}}_{text{5}}^{text{5}}$ = 5.(5 – 1).(5 – 2).(5 – 3).(5 – 4) = 5 . 4 . 3 . 2 . 1 = 120 số
c) cách chọn ra ba chữ số trong 5 chữ số trên là tổ hợp chập 3 của 5 phần tử:
$ mathop{text{C}}_{text{5}}^{text{3}}=frac{text{5}text{.(5 – 1)}text{.(5 – 2) }}{text{3!}}=frac{text{ 5 }text{. 4 }text{. 3}}{text{3}text{.(3 – 1)(3 – 2)}}=frac{60}{6}=10$ nhóm
2. Ví dụ 2:
Cho 5 chữ số 1, 2, 3, 4, 5. Dùng 5 chữ số này:
a) Lập được bao nhiêu số tự nhiên có 4 chữ số trong đó không có chữ số nào lặp lại? Tính tổng các số lập được
b) lập được bao nhiêu số chẵn có 5 chữ số khác nhau?
c) Lập được bao nhiêu số tự nhiên có 5 chữ số, trong đó hai chữ số kề nhau phải khác nhau
d) Lập được bao nhiêu số tự nhiên có 4 chữ số, các chữ số khác nhau, trong đó có hai chữ số lẻ, hai chữ số chẵn
Giải
a) số tự nhiên có 4 chữ số, các chữ số khác nhau, lập bởi 4 trong các chữ số trên là chỉnh hợp chập 4 của 5 phần tử:
$ displaystyle mathop{text{A}}_{text{5}}^{text{4}}$ = 5.(5 – 1).(5 – 2).(5 – 3) = 5 . 4 . 3 . 2 = 120 số
. 3 . 2 = 120 số
Trong mỗi hàng (Nghìn, trăm, chục, đơn vị), mỗi chữ số có mặt: 120 : 5 = 24 lần
Tổng các chữ số ở mỗi hang: (1 + 2 + 3 + 4 + 5). 24 = 15 . 24 = 360
Tổng các số được lập: 360 + 3600 + 36000 + 360000 = 399960
b) chữ số tận cùng có 2 cách chọn (là 2 hoặc 4)
bốn chữ số trước là hoán vị của của 4 chữ số còn lại và có P4 = 4! = 4 . 3 . 2 = 24 cách chọn
Tất cả có 24 . 2 = 48 cách chọn
c) Các số phải lập có dạng $ overline{text{ abcde}}$, trong đó : a có 5 cách chọn, b có 4 cách chọn (khác a), c có 4 cách chọn (khác b), d có 4 cách chọn (khác c), e có 4 cách chọn (khác d)
Tất cả có: 5 . 4 . 4 . 4 . 4 = 1280 số
d) Chọn 2 trong 2 chữ số chẵn, có 1 cách chọn
chọn 2 trong 3 chữ số lẻ, có 3 cách chọn. Các chữ số có thể hoán vị, do đó có:
1 . 3 . 4! =1 . 3 . 4 . 3 . 2 = 72 số
3. Ví dụ 3: Cho $ widehat{text{xAy }}ne {{180}^{0}}$ . Trên Ax lấy 6 điểm khác A, trên Ay lấy 5 điểm khác A. trong 12 điểm nói trên (kể cả điểm A), hai điểm nào củng được nối với nhau bởi một đoạn thẳng.
Có bao nhiêu tam giác mà các đỉnh là 3 trong 12 điểm ấy
Giải
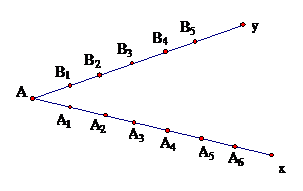
Cách 1: Tam giác phải đếm gồm ba loại:
+ Loại 1: các tam giác có một đỉnh là A, đỉnh thứ 2 thuộc Ax (có 6 cách chọn), đỉnh thứ 3 thuộc Ay (có 5 cách chọn), gồm có: 6 . 5 = 30 tam giác
+ Loại 2: Các tam giác có 1 đỉnh là 1 trong 5 điểm B1, B2, B3, B4, B5 (có 5 cách chọn), hai đỉnh kia là 2 trong 6 điểm A1, A2, A3, A4, A5, A6 ( Có $ displaystyle mathop{text{C}}_{text{6}}^{text{2}}=frac{6.5}{2!}=frac{30}{2}=15$ cách chọn)
Gồm 5 . 15 = 75 tam giác
+ Loại 3: Các tam giác có 1 đỉnh là 1 trong 6 điểm A1, A2, A3, A4, A5, A6 hai đỉnh kia là 2 trong 5 điểm B1, B2, B3, B4, B5 gồm có: 6.$ displaystyle mathop{text{C}}_{text{5}}^{text{2}}=6.frac{5.4}{2!}=6.frac{20}{2}=60$ tam giác.
Tất cả có: 30 + 75 + 60 = 165 tam giác
Cách 2: số các tam giác chọn 3 trong 12 điểm ấy là
$ displaystyle mathop{text{C}}_{text{12}}^{text{3}}=frac{12.11.10}{3!}=frac{1320}{3.2}=frac{1320}{6}=220$
Số bộ ba điểm thẳng hang trong 7 điểm thuộc tia Ax là:
$ displaystyle mathop{text{C}}_{text{7}}^{text{3}}=frac{7.6.5}{3!}=frac{210}{3.2}=frac{210}{6}=35$
Số bộ ba điểm thẳng hang trong 6 điểm thuộc tia Ay là:
$ displaystyle mathop{text{C}}_{text{6}}^{text{3}}=frac{6.5.4}{3!}=frac{120}{3.2}=frac{120}{6}=20$
Số tam giác tạo thành: 220 – ( 35 + 20) = 165 tam giác
D. BÀI TẬP:
Bài 1: cho 5 số: 0, 1, 2, 3, 4. từ các chữ số trên có thể lập được bao nhiêu số tự nhiên:
a) Có 5 chữ số gồm cả 5 chữ số ấy?
b) Có 4 chữ số, có các chữ số khác nhau?
c) có 3 chữ số, các chữ số khác nhau?
d) có 3 chữ số, các chữ số có thể giống nhau?
Bài 2: Có bao nhiêu số tự nhiên có 4 chữ số lập bởi các chữ số 1, 2, 3 biết rằng số đó chia hết cho 9
Bài 3: Trên trang vở có 6 đường kẻ thẳng đứng và 5 đường kẻ nằm ngang đôi một cắt nhau. Hỏi trên trang vở đó có bao nhiêu hình chữ nhật.
