Lý thuyết hàm số bậc 2
1. Định nghĩa hàm số bậc 2
Hàm số bậc hai là hàm số có công thức: $displaystyle y=ax_{{}}^{2} bx c$ ( với a ≠ 0)
Tập xác định (TXĐ): D = R.
2. Tính biến thiên của hàm số bậc 2
Bảng biến thiên của hàm số:
a > 0 hàm số nghịch biến trên $displaystyle left( {-infty ;-frac{b}{{2a}}} right)$ và đồng biến trên khoảng $displaystyle left( {-frac{b}{{2a}}; infty } right)$
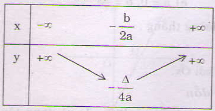
a
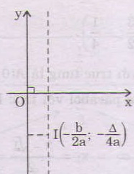
Đồ thị hàm số $displaystyle y=ax_{{}}^{2} bx c$ là một đường parabol (P) có:
Tọa độ đỉnh I $displaystyle left( {frac{{-b}}{{2a}};fleft( {frac{{-b}}{{2a}}} right)} right)$
với $displaystyle {fleft( {frac{{-b}}{{2a}}} right)}$ = $displaystyle frac{{-Delta }}{{4a}}$
Trục đối xứng : x = $displaystyle frac{{-b}}{{2a}}$
Parabol (P) quay bề lõm lên trên nếu a > 0, parabol (P) quay bề lõm xuống dưới nếu a