Đề thi tuyển sinh vào lớp 10 môn Toán TP. Hồ Chí Minh năm học 2014-2015
Thời gian làm bài: 120 phút (không kể thời gian giao đề)
Bài 1: (2 điểm)
Giải các phương trình và hệ phương trình sau:
a) $ displaystyle {{x}^{2}}-7x+12=0$
b) $ displaystyle {{x}^{2}}-(sqrt{2}+1)x+sqrt{2}=0$
c) $ displaystyle {{x}^{4}}-9{{x}^{2}}+20=0$
d) $ displaystyle left{ begin{matrix}3x-2y=4 4x-3y=5 end{matrix} right.$
Bài 2: (1,5 điểm)
a) Vẽ đồ thị (P) của hàm số và đường thẳng (D): trên cùng một hệ trục toạ độ.
b) Tìm toạ độ các giao điểm của (P) và (D) ở câu trên bằng phép tính.
Bài 3: (1,5 điểm)
Thu gọn các biểu thức sau:
$ displaystyle A=frac{5+sqrt{5}}{sqrt{5}+2}+frac{sqrt{5}}{sqrt{5}-1}-frac{3sqrt{5}}{3+sqrt{5}}$
$ displaystyle B=left( frac{x}{x+3sqrt{x}}+frac{1}{sqrt{x}+3} right):left( 1-frac{2}{sqrt{x}}+frac{6}{x+3sqrt{x}} right)$ (x > 0)
Bài 4: (1,5 điểm)
Cho phương trình $ displaystyle {{x}^{2}}-mx-1=0$ (1) (x là ẩn số)
- a) Chứng minh phương trình (1) luôn có 2 nghiệm trái dấu
- b) Gọi x1, x2 là các nghiệm của phương trình (1):
Tính giá trị của biểu thức:
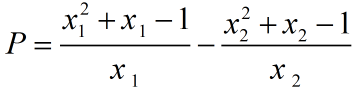
Bài 5: (3,5 điểm)
Cho tam giác ABC có ba góc nhọn, nội tiếp đường tròn tâm O (AB < AC). Các đường cao AD và CF của tam giác ABC cắt nhau tại H.
a) Chứng minh tứ giác BFHD nội tiếp. Suy ra $ displaystyle widehat{AHC}={{180}^{0}}-widehat{ABC}$
b) Gọi M là điểm bất kì trên cung nhỏ BC của đường tròn (O) (M khác B và C) và N là điểm đối xứng của M qua AC. Chứng minh tứ giác AHCN nội tiếp.
c) Gọi I là giao điểm của AM và HC; J là giao điểm của AC và HN. Chứng minh $ displaystyle widehat{AJI}=widehat{ANC}$
d) Chứng minh rằng : OA vuông góc với IJ
Gợi ý giải:
Bài 1: (2 điểm)
Giải các phương trình và hệ phương trình sau:
a) $ displaystyle {{x}^{2}}-7x+12=0$
$ displaystyle Delta ={{7}^{2}}-4.12=1$
$ displaystyle Leftrightarrow x=frac{7+1}{2}=4,,,hay,,,x=frac{7-1}{2}=3$
b) $ displaystyle {{x}^{2}}-(sqrt{2}+1)x+sqrt{2}=0$
Phương trình có : a + b + c = 0 nên có 2 nghiệm là: $ displaystyle x=1,,hay,,,x=frac{c}{a}=sqrt{2}$
c) $ displaystyle {{x}^{4}}-9{{x}^{2}}+20=0$
Đặt u = x2 ≥ 0 pt thành: $ displaystyle {{u}^{2}}-9u+20=0,Leftrightarrow (u-4),(u-5)=0$
$ displaystyle Leftrightarrow u=4,,,hay,,u=5$
Do đó pt $ displaystyle Leftrightarrow {{x}^{2}}=4,,hay,{{x}^{2}}=5Leftrightarrow x=pm 2,,,hay,,x=pm sqrt{5}$
d) $ displaystyle left{ begin{matrix}3x-2y=4 4x-3y=5 end{matrix} right.$
⇔ $ displaystyle left{ begin{matrix}12x-8y=16,,, 12x-9y=15,,,, end{matrix} right.$
⇔ $ displaystyle left{ begin{matrix}y=1 x=2 end{matrix} right.$
Bài 2:
a) Đồ thị:
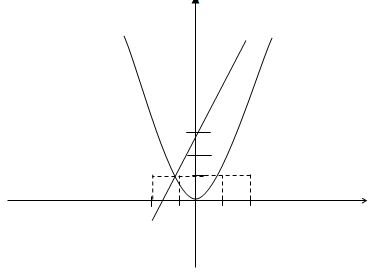
Lưu ý: (P) đi qua O(0;0), $ displaystyle left( pm 1;1 right),left( pm 2;4 right)$
(D) đi qua (-1;1) , (3;9)
b) PT hoành độ giao điểm của (P) và (D) là
x2 = 2x +3 ⇔ x2 – 2x – 3 = 0 ⇔ x = -1 hay x = 3 (do a-b+c=0)
y(-1) = 1, y(3) = 9
Vậy toạ độ giao điểm của (P) và (D) là (-1;1) , (3;9)
Bài 3: Thu gọn các biểu thức sau
$ displaystyle A=frac{5+sqrt{5}}{sqrt{5}+2}+frac{sqrt{5}}{sqrt{5}-1}-frac{3sqrt{5}}{3+sqrt{5}}$
= $ displaystyle frac{(5+sqrt{5})(sqrt{5}-2)}{(sqrt{5}+2)(sqrt{5}-2)}+frac{sqrt{5}(sqrt{5}+1)}{(sqrt{5}-1)(sqrt{5}+1)}-frac{3sqrt{5}(3-sqrt{5})}{(3+sqrt{5})(3-sqrt{5})}$
= $ displaystyle 3sqrt{5}-5+frac{5+sqrt{5}}{4}-frac{9sqrt{5}-15}{4}=3sqrt{5}-5+frac{5+sqrt{5}-9sqrt{5}+15}{4}$
= $ displaystyle 3sqrt{5}-5+5-2sqrt{5}=sqrt{5}$
Bài 4:
Cho phương trình $ displaystyle {{x}^{2}}-mx-1=0$ (1) (x là ẩn số)
a) Chứng minh phương trình (1) luôn có 2 nghiệm trái dấu
Ta có a.c = -1 < 0 , với mọi m nên phương trình (1) luôn có 2 nghiệm trái dấu với mọi m.
b) Gọi x1, x2 là các nghiệm của phương trình (1):
Tính giá trị của biểu thức:
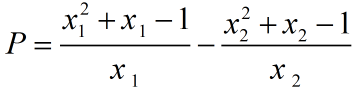
Ta có $ displaystyle x_{1}^{2}=m{{x}_{1}}+1,,$ và $ displaystyle x_{2}^{2}=m{{x}_{2}}+1,,$ (do x1, x2 thỏa 1)
Do đó:
![]()
Bài 5:
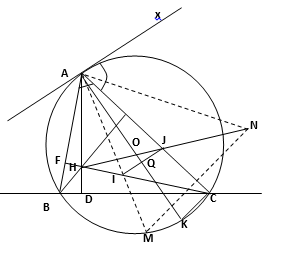
a) Ta có tứ giác BFHD nội tiếp do có 2 góc đối
F và D vuông ⇒ $ displaystyle widehat{FHD}=widehat{AHC}={{180}^{0}}-widehat{ABC}$
b) $ displaystyle widehat{ABC}=widehat{AMC}$ cùng chắn cung AC
mà $ displaystyle widehat{ANC}=widehat{AMC}$ do M, N đối xứng
Vậy ta có $ displaystyle widehat{AHC,}$ và $ displaystyle widehat{ANC,}$ bù nhau
⇒ tứ giác AHCN nội tiếp
c) Ta sẽ chứng minh tứ giác AHIJ nội tiếp
Ta có $ displaystyle widehat{NAC}=widehat{MAC}$ do MN đối xứng qua AC mà $ displaystyle widehat{NAC}=widehat{CHN}$ (do AHCN nội tiếp)
⇒ $ displaystyle widehat{IAJ}=widehat{IHJ}$ ⇒ tứ giác HIJA nội tiếp.
⇒ $ displaystyle widehat{AJI}$ bù với $ displaystyle widehat{AHI,}$ mà $ displaystyle widehat{ANC}$ bù với $ displaystyle widehat{AHI,}$ (do AHCN nội tiếp)
⇒ $ displaystyle widehat{AJI}=widehat{ANC}$
Cách 2 :
Ta sẽ chứng minh IJCM nội tiếp
Ta có $ displaystyle widehat{AMJ}$ = $ displaystyle widehat{ANJ}$ do AN và AM đối xứng qua AC.
Mà $ displaystyle widehat{ACH}$ = $ displaystyle widehat{ANH}$ (AHCN nội tiếp) vậy $ displaystyle widehat{ICJ}$ = $ displaystyle widehat{IMJ}$
⇒ IJCM nội tiếp ⇒ $ displaystyle widehat{AJI}=widehat{AMC}=widehat{ANC}$
d) Kẻ OA cắt đường tròn (O) tại K và IJ tại Q ta có $ displaystyle widehat{AJQ}$ = $ displaystyle widehat{AKC}$
vì $ displaystyle widehat{AKC}$ = $ displaystyle widehat{AMC}$ (cùng chắn cung AC), vậy $ displaystyle widehat{AKC}$ = $ displaystyle widehat{AMC}$ = $ displaystyle widehat{ANC}$
Xét hai tam giác AQJ và AKC :
Tam giác AKC vuông tại C (vì chắn nửa vòng tròn ) 2 tam giác trên đồng dạng
Vậy $ displaystyle widehat{Q}={{90}^{0}}$ . Hay AO vuông góc với IJ
Cách 2 : Kẻ thêm tiếp tuyến Ax với vòng tròn (O) ta có $ displaystyle widehat{xAC}$ = $ displaystyle widehat{AMC}$
mà $ displaystyle widehat{AMC}$ = $ displaystyle widehat{AJI}$ do chứng minh trên vậy ta có $ displaystyle widehat{xAC}$ = $ displaystyle widehat{AJQ}$ ⇒ JQ song song Ax
Vậy IJ vuông góc AO (do Ax vuông góc với AO).
