BÀI TẬP TUẦN 2
– Liên hệ giữa phép nhân (phép chia ) và phép khai phương
– 1 số hệ thức cạnh và đường cao trong tam giác vuông
Bài 1: Tính
a) $ displaystyle sqrt{90.360}$
b) $ displaystyle sqrt{52}.sqrt{13}$
c) $ displaystyle sqrt{frac{{{65}^{2}}-{{52}^{2}}}{196}}$
d) $ displaystyle frac{sqrt{13}}{sqrt{208}}$
Bài 2: Thực hiện phép tính
a) $ displaystyle sqrt{1,6}.sqrt{250}+sqrt{19,6}:sqrt{4,9}$
b)$ displaystyle left( sqrt{frac{2}{3}}+sqrt{frac{50}{3}}-sqrt{24} right).sqrt{6}$
c) $ displaystyle left( sqrt{frac{1}{3}}-sqrt{frac{4}{3}}+sqrt{3} right):sqrt{3}$
d) $ displaystyle sqrt{3+sqrt{5}}.sqrt{2}$
Bài 3: Rút gọn biểu thức:
a) $ displaystyle frac{sqrt{10}-sqrt{15}}{sqrt{8}-sqrt{12}}$
b) $ displaystyle frac{5+sqrt{5}}{sqrt{10}+sqrt{2}}$
c) $ displaystyle frac{xsqrt{y}+ysqrt{x}}{x+2sqrt{xy}+y}$( với x ≥ 0, y ≥ 0, xy ≠ 0
d) $ displaystyle frac{xsqrt{x}+ysqrt{y}}{x-sqrt{xy}+y}$
Bài 4: Rút gọn biểu thức sau:
a) A = $ displaystyle sqrt{8+2sqrt{15}}-sqrt{8-2sqrt{15}}$
b) B = $ displaystyle sqrt{3-sqrt{5}}-sqrt{3+sqrt{5}}$( 2 cách)
c*) C =$ displaystyle sqrt{2+sqrt{3}}.sqrt{2+sqrt{2+sqrt{3}}}.sqrt{2+sqrt{2+sqrt{2+sqrt{3}}}}.sqrt{2-sqrt{2+sqrt{2+sqrt{3}}}}$
d) $ displaystyle frac{sqrt{15}-sqrt{5}}{sqrt{3}-1}+frac{5-2sqrt{5}}{2sqrt{5}-4}$
e) $ displaystyle frac{3+2sqrt{3}}{sqrt{3}}+frac{2+sqrt{2}}{sqrt{2}+1}-(sqrt{2}+sqrt{3})$
Bài 5: Tìm x, biết:
a) $ displaystyle sqrt{x-5}+sqrt{4x-20}-frac{1}{5}sqrt{9x-45}=3$
b) $ displaystyle 2sqrt{9x-27}-frac{1}{5}sqrt{25x-75}-frac{1}{7}sqrt{49x-147}=20$
c) $ displaystyle sqrt{{{x}^{2}}-2x+9}=2x-3$
d)$ displaystyle sqrt{6-2{{x}^{2}}}+1=x$
e) $ displaystyle sqrt{x-3}-2sqrt{{{x}^{2}}-9}=0$
f) $ displaystyle frac{sqrt{x-3}}{sqrt{2x+1}}=2$
Bài 6*: Tìm giá trị lớn nhất của biểu thức
a) A = $ displaystyle frac{sqrt{{{x}^{2}}+x+3}}{sqrt{{{x}^{2}}+x+1}}$
b) B = $ displaystyle sqrt{1-x}.sqrt{x+3}$
Bài 7: Tìm x, y có trên hình vẽ sau :
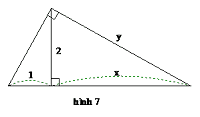
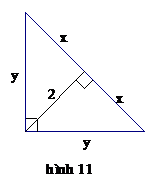
Bài 9*: Cho tam giác ABC cân tại A, đường cao AH và BK. Chứng minh:
$ displaystyle frac{1}{B{{K}^{2}}}=frac{1}{B{{C}^{2}}}+frac{1}{4A{{H}^{2}}}$
