Toán cấp 2 nhắc lại lý thuyết về hình chữ nhật cùng các dạng toán liên quan với những bài tập có lời giải. Giúp các em lớp 8 ôn tập bồi dưỡng tốt.
Mục tiêu:
– Giúp học sinh nắm được định nghĩa hình chữ nhật , các tính chất của hình chữ nhật, các dấu hiệu nhận biết một tứ giác là hình chữ nhật.
– Học sinh biết vẽ hình chữ nhật, biết chứng minh một tứ giác là hình chữ nhật, biết vận dụng các kiến thức về hình chữ nhật để giải toán.
– Rèn cho học sinh kĩ năng suy luận, vận dụng tính chất của hình chữ nhật để chứng minh các đoạn thẳng bằng nhau, các góc bằng nhau, chứng minh ba điểm thẳng hàng, hai đường thẳng song song.
A. Tóm tắt lý thuyết
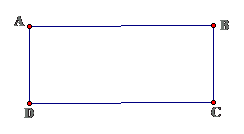
1. Định nghĩa: Hình chữ nhật là tứ giác có bốn góc vuông
$ displaystyle diamond ABCD$ là hình chữ nhật $ displaystyle Leftrightarrow left{ begin{array}{l}diamond ABCDhat{A}=hat{B}=hat{C}=hat{D}end{array} right.$
– Nhận xét: Hình chữ nhật cũng là 1 hình bình hành, 1 hình thang cân
2. Tính chất: Hình chữ nhật có tất cả các tính chất của hình bình hành và hình thang cân
– Tính chất về cạnh: Các cạnh đối bằng nhau, song song với nhau
– Tính chất về góc: Bốn góc bằng nhau
– Tính chất về đường chéo: Hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường
3. Dấu hiệu nhận biết
– Tứ giác có ba góc vuông là hình chữ nhật
– Hình thang cân có 1 góc vuông là hình chữ nhật
– Hình bình hành có 1 góc vuông là hình chữ nhật
– Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật
4. Ứng dụng vào tam giác vuông
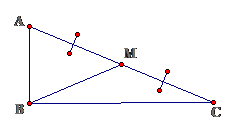
– Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền, ta có: $ displaystyle BM=frac{1}{2}AC$
– Nếu một tam giác có đường trung tuyến ứng với 1 cạnh bằng nửa cạnh ấy thì tam giác đó là tam giác vuông: $ displaystyle BM=frac{1}{2}ACRightarrow Delta ABC$ vuông.
B. Bài tập và các dạng toán
Dạng 1: Chứng minh 1 tứ giác là hình chữ nhật
Cách giải: Vận dụng các dấu hiệu nhận biết để chứng minh 1 tứ giác là hình chữ nhật
Bài 1: Cho tứ giác ABCD có $ displaystyle ACbot BDequiv O$. Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Chứng minh rằng:
a. OE + OF + OG + OH bằng nửa chu vi tứ giác ABCD
b. Tứ giác EFGH là hình chữ nhật
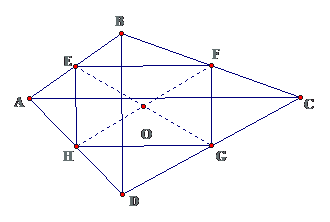
Lời giải
a. Ta có
$ displaystyle OE+text{OF+OG+OH=}frac{text{1}}{text{2}}(AB+BC+CD+DA)=frac{1}{2}{{P}_{ABCD}}$
b. Có $ displaystyle left{ begin{array}{l}text{EF//GH}text{EF=G}end{array} right.Rightarrow diamond text{EFGH}$ là hình bình hành ( dấu hiệu nhận biết )
Mặt khác $ displaystyle left{ begin{array}{l}ACbot BDAC//text{EF}end{array} right.Rightarrow left{ begin{array}{l}text{EF}bot text{BD}text{BD//EH}end{array} right.Rightarrow EHbot text{EF}Rightarrow diamond text{EFGH}$ là hình chữ nhật (dhnb)
Bài 2: Cho tam giác ABC vuông cân tại C. Trên cạnh AC, BC lấy lần lượt các điểm P, Q sao cho AP = CQ. Từ điểm P vẽ PM // BC ( M thuộc AB ). Chứng minh tứ giác PCQM là hình chữ nhật.
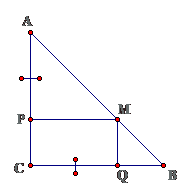
Lời giải
Ta có $ displaystyle Delta ABC$ vuông cân $ displaystyle Rightarrow hat{A}={{45}^{0}}Rightarrow Delta APM$ vuông cân $ displaystyle Rightarrow AP=PM$
Theo giải thiết $ displaystyle AP=CQRightarrow PM=CQ$
Lại có $ displaystyle PM//CQRightarrow diamond PMCQ$ là hình bình hành
Mặt khác $ displaystyle hat{C}={{90}^{0}}Rightarrow diamond PMCQ$ là hình chữ nhật (dhnb)
Bài 3: Cho hình chữ nhật ABCD, E thuộc AD, F thuộc AB. Gọi I, K, M, N theo thứ tự là trung điểm của EF, DF, BE, BD. Chứng minh rằng IN = KM.
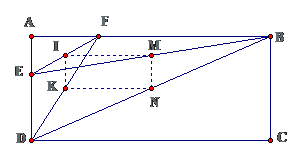
Lời giải
Ta đi chứng minh tứ giác IKMN là hình chữ nhật
+) Theo giả thiết có : $ displaystyle left{ begin{array}{l}IM//KN(//FB)IM=KN=frac{1}{2}FBend{array} right.Rightarrow diamond IMKN$
Là hình bình hành (dhnb)
+) $ displaystyle left{ begin{array}{l}IK//DAADbot ABend{array} right.Rightarrow left{ begin{array}{l}IKbot ABIM//ABend{array} right.Rightarrow IMbot IKRightarrow diamond IKMN$ là hình chữ nhật $ displaystyle Rightarrow IN=KM$
Bài 4: Cho tam giác ABC vuông tại A, AB < AC, đường cao AH. Lấy điểm E trên cạnh AC sao cho AE = AB. Gọi I là trung điểm của BE, kẻ $ displaystyle EKbot BC(Kin BC),ENbot AH(Nin AH)$.
a. Chứng minh tứ giác NEKH là hình chữ nhật
b. $ displaystyle Ihat{H}A=Ihat{H}C$
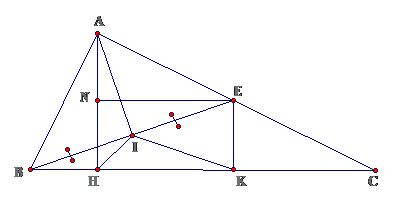
Lời giải
a. Tứ giác NEKH có 3 góc vuông nên là hình chữ nhật
b. Ta đi chứng minh $ displaystyle Delta IHA=Delta IHK$
Xét $ displaystyle Delta IHA,Delta IHK:$ IH cạnh chung , $ displaystyle AI=IK=frac{1}{2}BE$
Cần thêm AH = HK hoặc AH = NE ( do HK = NE )
$ displaystyle Delta ABH=Delta AEN(ch-gn)Rightarrow AH=NE$
⇒ $ displaystyle AH=HKRightarrow Delta IHA=Delta IHKRightarrow Ihat{H}A=Ihat{H}C$
Dạng 2: Vận dụng tính chất của HCN để chứng minh qua hệ bằng nhau, song song, vuông góc, tính độ dài các đoạn thẳng
Cách giải: Áp dụng các tính chất của hình chữ nhật
– Áp dụng tính chất đường trung tuyến trong tam giác vuông
Bài 5: Cho hình chữ nhật ABCD, AB = 40cm, O là giao điểm của hai đường chéo. Gọi H là chân đường vuông góc kẻ từ A đến BD. Tính độ dài đoạn DH, OH, OB.
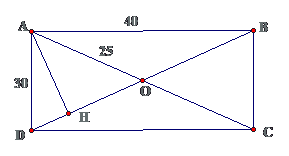
Lời giải
Áp dụng định lý pytago $ displaystyle Rightarrow BD=50cm$
$ displaystyle OA=OB=OC=OD=25cm$
$ displaystyle A{{D}^{2}}-D{{H}^{2}}=A{{H}^{2}}=A{{O}^{2}}-H{{O}^{2}}=A{{O}^{2}}-{{(D{{O}^{2}}-DH)}^{2}}$
Hay $ displaystyle begin{array}{l}{{30}^{2}}-D{{H}^{2}}={{25}^{2}}-{{(25-DH)}^{2}}Leftrightarrow {{30}^{2}}-D{{H}^{2}}={{25}^{2}}-(625-50DH+D{{H}^{2}})Leftrightarrow 50DH=900Rightarrow DH=18Rightarrow HO=7CMend{array}$
Cách 2:
$ displaystyle {{S}_{ABD}}=frac{1}{2}AD.AB=600=frac{1}{2}AH.BD$
⇒ $ displaystyle 600=frac{1}{2}.50.AHRightarrow AH=24Rightarrow DH=18cm$
Bài 6: Cho hình chữ nhật ABCD. Gọi E là chân đường vuông góc kẻ từ B đến AC. I là trung điểm của AE, M là trung điểm của CD, H là trung điểm của BE.
a. Chứng minh rằng CH // IM
b. Tính góc BIM
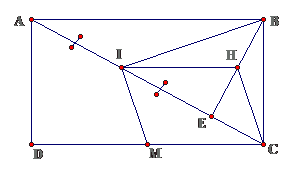
Lời giải
a. Ta có IH là đường trung bình $ displaystyle Delta AEBRightarrow left{ begin{array}{l}IH//ABIH=frac{1}{2}ABend{array} right.$
Lại có $ displaystyle left{ begin{array}{l}MN//ABMN=frac{1}{2}ABend{array} right.Rightarrow diamond IMCH$ là hình bình hành $ displaystyle Rightarrow CH//IM$
Ta có: $ displaystyle IH//MC,MCbot BCRightarrow IHbot BC$
Xét $ displaystyle Delta IBC$ có H là trực tâm $ displaystyle Rightarrow left{ begin{array}{l}CHbot BICH//IMend{array} right.Rightarrow Bhat{I}M={{90}^{0}}$
Bài 7: Cho hình chữ nhật ABCD. Lấy điểm P tùy ý trên đường chéo BD. Gọi M là điểm đối xứng của C qua P.
a. Chứng minh AM // BD
b. Gọi E, F lần lượt là hình chiếu của M trên AD, AB. Chứng minh AEMF là hình chữ nhật
c. EF // AC
d. E, F, P thẳng hàng
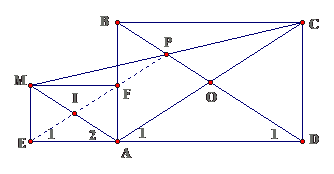
Lời giải
a. Gọi O là giao điểm của BD và AC
Ta có OP là đường trung bình của $ displaystyle Delta AMCRightarrow OP//AM$
b. Xét $ displaystyle diamond AEMF$, có $ displaystyle hat{E}=hat{A}=hat{F}={{90}^{0}}Rightarrow diamond AEMF$ là hình chữ nhật
c. Ta có $ displaystyle {{hat{A}}_{2}}={{hat{D}}_{1}}(slt),{{hat{A}}_{2}}={{hat{E}}_{1}},{{hat{E}}_{1}}={{hat{A}}_{1}}(dvi)Rightarrow {{hat{E}}_{1}}={{hat{A}}_{1}}Rightarrow text{EF //AC}$
d. E, F, P thẳng hàng $ displaystyle IE//AC,text{IP//AC}Leftarrow $ IP là đường trung bình $ displaystyle Delta AMC$
Lại có EF // AC $ displaystyle Rightarrow IE//AC$
Theo tiên đề Ơclit thì E, F, P thẳng hàng
Bài 8: Cho tam giác ABC cân tại A. Từ điểm D trên đáy BC kẻ đường vuông góc với BC cắt AB ở E và AC ở F. Vẽ các hình chữ nhật DBHE và CDFK. Gọi I là tâm của hình chữ nhật BDEH, J là tâm của hình chữ nhật CDFK. Chứng minh rằng:
a. AIDJ và AHIJ là các hình chữ nhật
b. A, H, D thẳng hàng và A là trung điểm của HK
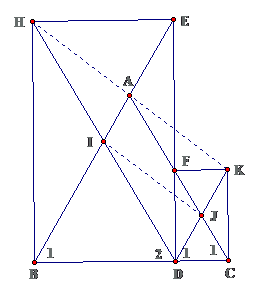
Lời giải
a. $ displaystyle diamond AIDJ$là hình bình hành $ displaystyle Rightarrow left{ begin{array}{l}AI//DJ({{{hat{B}}}_{1}}={{{hat{D}}}_{1}}={{{hat{C}}}_{1}})text{AJ//DI(}{{{text{hat{C}}}}_{text{1}}}={{{hat{D}}}_{2}}={{{hat{B}}}_{1}})end{array} right.$
$ displaystyle diamond AHtext{IJ}$là hình bình hành $ displaystyle Rightarrow left{ begin{array}{l}HI//AJ(HD//AC)text{AJ//HI(=ID})end{array} right.$
b. $ displaystyle A,H,K$thẳng hàng $ displaystyle Rightarrow diamond text{AIJK}$là HBH $ displaystyle Rightarrow left{ begin{array}{l}AI//KJ(AI//DJ)AI=KJ(AI=DJ)end{array} right.$
Vậy qua A có HA // IJ, KA // IJ nên A, H, K thẳng hàng.
Dạng 3: Sử dụng định lý thuận và đảo của đường trung tuyến ứng với cạnh huyền trong tam giác vuông
Cách giải: Sử dụng định lý về tính chất đường trung tuyến ứng với cạnh huyền của tam giác vuông để chứng minh các hình bằng nhau hoặc chứng minh tam giác vuông
Bài 9: Cho tam giác ABC, các đường cao BD và CE. Gọi M, N là chân các đường vuông góc kẻ từ B, C đến DE. Gọi I là trung điểm của DE, K là trung điểm của BC. Chứng minh rằng:
a. $ displaystyle IKbot ED$
b. EM = DN
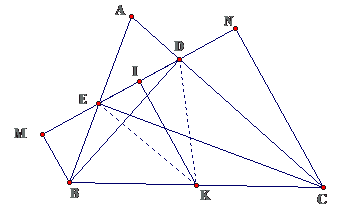
Lời giải
a. Ta có $ displaystyle EK=DK=frac{1}{2}BCRightarrow left{ begin{array}{l}Delta EKD(KE=KD)IE=IDend{array} right.$
$ displaystyle Rightarrow IKbot ED(dpcm)$
b. $ displaystyle left{ begin{array}{l}KB=KC(Kin BC)KI//BM//NCend{array} right.Rightarrow KI$là đường trung bình của hình thang MBNC $ displaystyle Rightarrow left{ begin{array}{l}IM=INIE=IDend{array} right.Rightarrow ME=DN$
Bài 10: Cho tam giác ABC vuông tại A, đường cao AH. Gọi I, K theo thứ tự là trung điểm của AB, AC. Chứng minh:
a. $ displaystyle Ihat{H}K={{90}^{0}}$
b. Chu vi tam giác IHK bằng nửa chu vi tam giác ABC
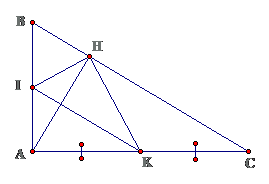
Lời giải
a. Ta có: $ displaystyle Delta IAH,Delta KAH$cân tại I và K $ displaystyle Rightarrow Ihat{A}H=Ihat{H}A,Hhat{A}K=Ahat{H}K$
$ displaystyle Rightarrow Ihat{H}A+Ahat{H}K={{90}^{0}}Rightarrow Ihat{H}K={{90}^{0}}$
b. Ta có $ displaystyle IH=frac{1}{2}AB,HK=frac{1}{2}BC,IK=frac{1}{2}BCRightarrow {{P}_{IHK}}=frac{1}{2}{{P}_{ABC}}(dpcm)$
Bài 11: Cho tam giác ABC có đường cao AI. Từ A kẻ tia Ax vuông góc với AC, từ B kẻ tia By song song với AC. Gọi M là giao điểm của hai tia Ax và By. Nối M với trung điểm P của AB, đường MP cắt AC tại Q và BQ cắt AI tại H.
a. Tứ giác AMBQ là hình gì
b. Chứng minh rằng CH vuông góc với AB
c. Chứng minh tam giác PIQ cân
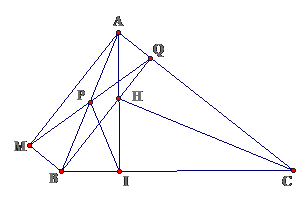
Lời giải
a. Ta có tứ giác AMBQ là hình chữ nhật ( hai đường chéo cắt nhau tại trung điểm của mỗi đường và bằng nhau )
b. Ta có H là trực tâm của $ displaystyle Delta ABCRightarrow CHbot AB$
c. có $ displaystyle PI=PQ=frac{1}{2}ABRightarrow Delta PIQ$ cân tại P.
Dạng 4: Tìm điều kiện để tứ giác là hình chữ nhật
Cách giải: Vận dụng định nghĩa, các tính chất và dấu hiệu nhận biết của hình chữ nhật
Bài 12: Cho tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA. Tìm điều kiện của tứ giác ABCD để tứ giác EFGH là hình chữ nhật.
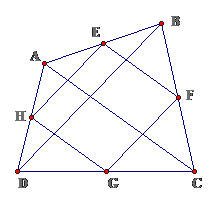
Lời giải
Ta có tứ giác EFGH là hình bình hành
Để EFGH trở thành hình chữ nhật thì :
$ displaystyle Rightarrow Htext{EF=9}{{text{0}}^{text{0}}}Rightarrow HEbot text{EF}Rightarrow text{AC}bot text{BD}$
Vậy điều kiện là hai đường chéo của tứ giác ABCD vuông góc với nhau.
Bài 13: Cho tam giác ABC. Gọi O là 1 điểm thuộc miền trong của tứ giác. M, N, P, Q lần lượt là trung điểm của các đoạn thẳng OB, OC, AC, AB
a. Chứng minh tứ giác MNPQ là hình bình hành
b. Xác định vị trí của điểm O để tứ giác MNPQ là hình chữ nhật
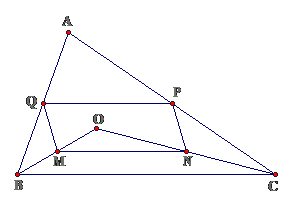
Lời giải
a. Ta có MNPQ là hình bình hành ( dấu hiệu nhận biết )
b. Để MNPQ trở thành hình bình hành thì O nằm trên đường cao xuất phát từ đỉnh A của $ displaystyle Delta ABC$
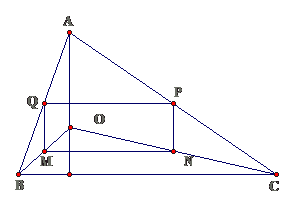
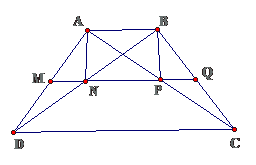
Bài 14: Cho hình thang cân ABCD ( AB // CD, AB < CD ). Gọi M, N, P, Q lần lượt là trung điểm của các đoạn thẳng AD, BD, AC, BC
a. Chứng minh bốn điểm M, N, P, Q thẳng hàng
b. Chứng minh tứ giác ABPN là hình thang cân
c. Tìm một hệ thức liên hệ giữa AB và CD để ABPN là hình chữ nhật
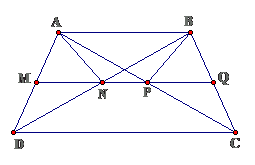
Lời giải
a. Ta có $ displaystyle MN//AB,MP//AB,PQ//AB,PN//ABRightarrow M,N,P,Q$
thẳng hàng nhau.
b. Hình thang ABPN có hai đường chéo bằng nhau nên là hình thang cân
c. Để ABPN là hình chữ nhật thì NP = AB hay CD = 3AB
BÀI TẬP VỀ NHÀ
Bài 1: Cho tam giác ABC, đường cao AH. Gọi I là trung điểm của AC. Lấy E là điểm đối xứng với H qua I. Gọi M, N lần lượt là trung điểm của HC, CE. Các đường thẳng AM, AN cắt HE tại G và K.
a. Chứng minh tứ giác AHCE là hình chữ nhật
b. Chứng minh HG = GK = KE
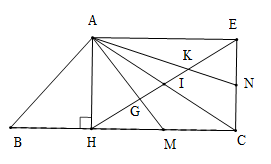Hướng dẫn
a. Chứng minh tứ giác AHCE là hình bình hành, có
$ displaystyle AHC={{90}^{0}}Rightarrow diamond AHCE$ là hình chữ nhật
b. Chứng minh G, K lần lượt là các trọng tâm của tam giác AHC, AEC và sử dụng tính chất 2 đường chéo của HCN
Bài 2: Cho tam giác ABC, các đường cao AD, BE, CF cắt nhau tại H, gọi I, K, R theo thứ tự là trung điểm của HA, HB, HC. Gọi M, N, P theo thứ tự là trung điểm của BC, AC, AB. Chứng minh rằng:
a. Tứ giác MNIK, PNRK là các hình chữ nhật
b. P, N, R, K, M, I cùng thuộc 1 đường tròn
c. D, E, F cũng thuộc đường tròn trên
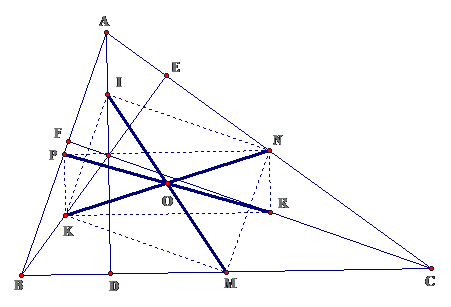
Lời giải
Ta có: $ displaystyle OD=frac{1}{2}IM,OE=frac{1}{2}KN,text{OF=}frac{text{1}}{text{2}}PR$
Bài 3: Cho tam giác ABC vuông tại A, M thuộc BC. Gọi D và E là chân đường vuông góc kẻ từ M đến AB và AC
a. Định dạng tứ giác ADME
b. Gọi I là trung điểm của DE. Chứng minh A, I, M thẳng hàng
c. Điểm M nằm ở đâu trên BC thì DE nhỏ nhất. Tính DE trong trường hợp đó biết AB = 15cm, AC =20cm
Lời giải
a. Tứ giác ADME có 3 góc vuông nên là hình chữ nhật
c. DE nhỏ nhất khi AM nhỏ nhất ( DE = AM ). AM nhỏ nhất khi và chỉ khi AM = AH khi M trùng H
Xét $ displaystyle Delta ABC$ vuông tại A
$ displaystyle Rightarrow BC=25cm(pytago)Rightarrow {{S}_{ABC}}=frac{1}{2}AH.BC=frac{1}{2}AB.ACRightarrow AH=frac{AB.AC}{BC}=frac{15.20}{25}=12(cm)$