BÀI 6: NGUYÊN LÍ ĐI-RÍCH-LÊ & NHỮNG BÀI TOÁN HÌNH HỌC THÚ VỊ
Nguyên lí có thể mở rộng như sau: Nếu có m vật đặt vào n cái ngăn kéo và m > k.n thì có ít nhất một ngăn kéo chứa ít nhất k + 1 vật. Với mở rộng này, ta còn có thể giải quyết thêm nhiều bài toán khác. Sau đây xin giới thiệu để bạn đọc làm quen việc vận dụng nguyên lí Đi-rích-lê với một số bài toán hình học.
Bài toán 1: Trong tam giác đều có cạnh bằng 4 (đơn vị độ dài, được hiểu đến cuối bài viết) lấy 17 điểm. Chứng minh rằng trong 17 điểm đó có ít nhất hai điểm mà khoảng cách giữa chúng không vượt quá 1

Lời giải: Chia tam giác đều có cạnh bằng 4 thành 16 tam giác đều có cạnh bằng 1 (hình 1). Vì 17 > 16, theo nguyên lí Đi-rích-lê, tồn tại ít nhất một tam giác đều cạnh bằng 1 có chứa ít nhất 2 điểm trong số 17 điểm đã cho. Khoảng cách giữa hai điểm đó luôn không vượt quá 1 (đpcm).
Bài toán 2: Trong một hình vuông cạnh bằng 7, lấy 51 điểm. Chứng minh rằng có 3 điểm trong 51 điểm đã cho nằm trong một hình tròn có bán kính bằng 1.
Lời giải: Chia hình vuông cạnh bằng 7 thành 25 hình vuông bằng nhau, cạnh của mỗi hình vuông nhỏ bằng 5/7 (hình 2).

Vì 51 điểm đã cho thuộc 25 hình vuông nhỏ, mà 51 > 2.25 nên theo nguyên lí Đi-rích-lê, có ít nhất một hình vuông nhỏ chứa ít nhất 3 điểm (3 = 2 + 1) trong số 51 điểm đã cho. Hình vuông cạnh bằng có bán kính đường tròn ngoại tiếp là:
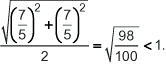
Vậy bài toán được chứng minh. Hình tròn này chính là hình tròn bán kính bằng 1, chứa hình vuông ta đã chỉ ra ở trên.
Bài toán 3: Trong mặt phẳng cho 2003 điểm sao cho cứ 3 điểm bất kì có ít nhất 2 điểm cách nhau một khoảng không vượt quá 1. Chứng minh rằng: tồn tại một hình tròn bán kính bằng 1 chứa ít nhất 1002 điểm.
Lời giải: Lấy một điểm A bất kì trong 2003 điểm đã cho, vẽ đường tròn C1 tâm A bán kính bằng 1.
+ Nếu tất cả các điểm đều nằm trong hình tròn C1 thì hiển nhiên có đpcm.
+ Nếu tồn tại một điểm B mà khoảng cách giữa A và B lớn hơn 1 thì ta vẽ đường tròn C2 tâm B bán kính bằng 1.
Khi đó, xét một điểm C bất kì trong số 2001 điểm còn lại. Xét 3 điểm A, B, C, vì AB > 1 nên theo giả thiết ta có AC ≤ 1 hoặc BC ≤ 1. Nói cách khác, điểm C phải thuộc C1 hoặc C2. => 2001 điểm khác B và A phải nằm trong C1 hoặc C2. Theo nguyên lí Đi-rích-lê ta có một hình tròn chứa ít nhất 1001 điểm. Tính thêm tâm của hình tròn này thì hình tròn này chính là hình tròn bán kính bằng 1 chứa ít nhất 1002 điểm trong 2003 điểm đã cho.
Bài toán 4: Cho hình bình hành ABCD, kẻ 17 đường thẳng sao cho mỗi đường thẳng chia ABCD thành hai hình thang có tỉ số diện tích bằng 1/3 . Chứng minh rằng, trong 17 đường thẳng đó có 5 đường thẳng đồng quy.
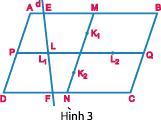
Lời giải: Gọi M, Q, N, P lần lượt là các trung điểm của AB, BC, CD, DA (hình 3).
Vì ABCD là hình bình hành => MN // AD // BC ; PQ // AB // CD.
Gọi d là một trong 17 đường thẳng đã cho. Nếu d cắt AB tại E ; CD tại F ; PQ tại L thì LP, LQ lần lượt là đường trung bình của các hình thang AEFD, EBCF. Ta có:
S(AEFD) / S(EBCF) = 1/3 hoặc S(EBCF) / S(EBFC) = 1/3 => LP / LQ = 1/3 hoặc là LQ / LP = 1/3.
Trên PQ lấy hai điểm L1, L2 thỏa mãn điều kiện L1P / L1Q = L2Q / L2P = 1/3 khi đó L trùng với L1 hoặc L trùng với L2. Nghĩa là nếu d cắt AB và CD thì d phải qua L1 hoặc L2.
Tương tự, trên MN lấy hai điểm K1, K2 thỏa mãn điều kiện K1M / K1N = K2N / K2M = 1/3 khi đó nếu d cắt AD và BC thì d phải qua K1 hoặc K2.
Tóm lại, mỗi đường thẳng trong số 17 đường thẳng đã cho phải đi qua một trong 4 điểm L1 ; L2 ; K1 ; K2.
Vì 17 > 4.4 nên theo nguyên lí Đi-rích-lê, trong 17 đường thẳng đó sẽ có ít nhất 5 đường thẳng (5 = 4 + 1) cùng đi qua một trong 4 điểm L1 ; L2 ; K1 ; K2 (5 đường thẳng đồng quy, đpcm).
Sau đây là một số bài tập tương tự.
Bài 1: Trong hình chữ nhật có kích thước 3 x 5, lấy 7 điểm bất kì. Chứng minh rằng có hai điểm cách nhau một khoảng không vượt quá $ displaystyle sqrt{5}$
Bài 2: Trong mặt phẳng tọa độ, cho ngũ giác lồi có tất cả các đỉnh là các điểm nguyên (có hoành độ và tung độ là số nguyên). Chứng minh rằng trên cạnh hoặc bên trong ngũ giác còn ít nhất một điểm nguyên khác nữa.
Bài 3: Tờ giấy hình vuông có cạnh bé nhất là bao nhiêu để có thể cắt ra được 5 hình tròn có bán kính bằng 1.
Bài 4: Trên một tờ giấy kẻ ô vuông, chọn 101 ô bất kì. Chứng minh rằng trong 101 ô đó có ít nhất 26 ô không có điểm chung.
BÀI 7: BÀN LUẬN VỀ BÀI TOÁN “BA VỊ THẦN”
Chúng ta đều đã biết bài toán thú vị: “Ba vị thần” sau:
Ngày xưa, trong một ngôi đền cổ có 3 vị thần giống hệt nhau. Thần thật thà (TT) luôn luôn nói thật, thần dối trá (DT) luôn luôn nói dối và thần khôn ngoan (KN) lúc nói thật lúc nói dối. Các vị thần vẫn trả lời câu hỏi của khách đến lễ đền nhưng không ai xác định được chính xác các vị thần. Một hôm có một nhà hiền triết từ xa đến thăm đền. Để xác định được các vị thần, ông hỏi thần bên trái:
– Ai ngồi cạnh ngài ?
– Đó là thần TT (1)
Ông hỏi thần ngồi giữa:
– Ngài là ai ?
– Ta là thần KN (2)
Sau cùng ông hỏi thần bên phải:
– Ai ngồi cạnh ngài ?
– Đó là thần DT (3)
Nhà hiền triết thốt lên:
– Tôi đã xác định được các vị thần.
Hỏi nhà hiền triết đã suy luận như thế nào ?
Lời giải: Gọi 3 vị thần theo thứ tự từ trái sang phải là: A, B, C.
Từ câu trả lời (1) => A không phải là thần TT.
Từ câu trả lời (2) => B không phải là thần TT.
Vậy C là thần TT. Theo (3) đ B là thần DT đ A là thần KN
Nhận xét: Cả 3 câu hỏi đều tập trung xác định thần B, phải chăng đó là cách hỏi “thông minh” của nhà hiền triết để tìm ra 3 vị thần ? Câu trả lời không phải, mà là nhà hiền triết gặp may do 3 vị thần đã trả lời câu hỏi không “khôn ngoan” !
Nếu 3 vị thần trả lời “khôn ngoan” nhất mà vẫn đảm bảo tính chất của từng vị thần thì sau 3 câu hỏi, nhà hiền triết cũng không thể xác định được vị thần nào. Ta sẽ thấy rõ hơn qua phân tích sau về 2 cách hỏi của nhà hiền triết:
- Hỏi thần X:
– Ngài là ai ?
Có 3 khả năng trả lời sau:
– Ta là thần TT => không xác định được X (Cách trả lời khôn nhất)
– Ta là thần KN => X là thần KN hoặc DT
– Ta là thần DT => X là KN
- Hỏi thần X:
– Ai ngồi cạnh ngài ?
Cũng có 3 khả năng trả lời sau:
– Đó là thần TT => thần X khác thần TT
– Đó là thần KN => không xác định được X (cách trả lời khôn nhất)
– Đó là thần DT => không xác định được X (cách trả lời khôn nhất)
Trong cả 2 cách hỏi của nhà hiền triết đều có cách trả lời khiến nhà hiền triết không có được một thông tin nào về ba vị thần thì làm sao mà xác định được các vị thần. Nếu gặp may (do sự trả lời ngờ nghệch) thì chỉ cần sau 2 câu hỏi nhà hiền triết cũng đủ để xác định 3 vị thần. Các bạn tự tìm xem trường hợp đó các câu trả lời của các vị thần là như thế nào nhé.
Bài toán cổ này thật là hay và dí dỏm, nhưng nếu các vị thần trả lời theo các phương án “khôn ngoan” nhất thì có cách nào để xác định được 3 vị thần sau 1 số ít nhất câu hỏi được không ?
Rõ ràng là không thể đặt câu hỏi như nhà hiền triết được.
Phải hỏi như thế nào để thu được nhiều thông tin nhất ?
Bây giờ ta đặt vấn đề như sau:
Mỗi lần hỏi chỉ được hỏi 1 vị thần và chính vị đó trả lời. Cần hỏi như thế nào để sau một số ít nhất câu hỏi ta xác định được các vị thần. Bài toán rõ ràng là không dễ chút nào, nhưng tôi tin rằng các bạn sẽ tìm ra nhiều phương án tối ưu đấy ! Sau đây là một phương án của tôi.
Hỏi thần A:
– Ngài là thần KN ?
– Nhận được câu trả lời.
Hỏi thần B:
– Ngài là thần KN ?
– Nhận được câu trả lời.
Sau đó tôi chỉ cần hỏi thêm 1 hoặc 2 câu nữa là xác định được chính xác 3 vị thần. Như vậy số câu hỏi nhiều nhất là 4. Các bạn có thể rút số câu hỏi xuống dưới 4 được không ?
Xin mời các bạn hãy giải trí bài toán này bằng một phương án tuyệt vời nào đó (Nhớ là chỉ hỏi một thần và chính vị đó trả lời).
