Dạng bài tập: Tìm điều kiện chia hết – Số học 6

Dạng bài tập Tìm điều kiện chia hết cũng là một dạng toán khó trong chương trình Toán lớp 6 ở phần Số học. Vì vậy các em cần phải chăm chỉ luyện tập dạng này.

Các em xem những ví dụ dưới đây rồi tự làm các bài tập tương tự.

Ví dụ 1:Tìm số nguyên n để giá trị của biểu thức A chia hết cho giá trị của biểu thức B:

A= n³ +2n² -3n+2 ,    B= n² -n

Giải: Đặt tính chia:

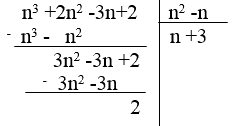
Muốn chia hết, ta phải có 2 chia hết cho n(n-1),do đó 2 chia hết cho n(vì n là số nguyên)

Ta có:

n	1	-1	2	-2
n-1	0	-2	1	-3
n(n-1)	0	2	2	6
	loại			loại

Vậy n= -1; n = 2

Ví dụ 2:

Tìm số nguyên dương n để n⁵ +1 chia hết cho n³ +1.

Giải: Ta có

n⁵ +1 chia hết cho  n³ +1

⇔ n² (n³+1) – (n² -1)  chia hết cho (n+1)(n² -n +1)

⇔ (n-1)(n+1) chia hết cho (n+1)(n² -n +1)

⇔ n -1  chia hết cho n² -n +1 (vì n+1 0)

Nếu n =1 thì ta được 0 chia hết cho 1

Nếu n>1 thì n -1< n(n-1) +1=n² -n +1, do đó không thể chia hết cho n² – n +1.

Vậy giá trị duy nhất của n tìm được là 1.

Ví dụ 3:

Tìm số nguyên n để n⁵ +1 chia hết cho n³+1.

Giải: Theo ví dụ trên ta có:

⇒ n -1 chia hết cho n² -n +1

⇒ n(n-1)   chia hết cho n² -n +1

⇒ n² -n     chia hết cho n² -n +1

⇒ (n² -n +1) -1  chia hết cho n² -n +1

⇒ 1 chia hết cho  n² -n +1

Có hai trường hợp

n² -n +1 =1 ⇔ n( n -1) =0 ⇔ n=0; n=1. Các giá trị này thoả mãn đề bài.

n² -n +1= -1 ⇔ n² -n +2 =0 không tìm được giá trị của n

Vậy n= 0; n =1 là hai số phải tìm.

Ví dụ 4:

Tìm số tự nhiên n sao cho 2ⁿ -1 chia hết cho 7.

Giải:

Nếu n = 3k (k ∈ N) thì 2ⁿ -1 = 2^3k -1 = 8^k -1

Chia hết cho 7

Nếu n =3k +1(k ∈ N) thì

2ⁿ -1= 2^3k+1 – 1=2(2^3k -1) +1 = Bs 7 +1

Nếu n = 3k +2 ( k ∈ N) thì

2ⁿ -1= 2^3k+2 -1 =4(2^3k – 1)+3 =Bs 7 +3

Vậy 2ⁿ -1 chia hết cho 7 n = 3k(k ∈ N).

*Bài tập áp dụng

Bài 1: Tìm điều kiện của số tự nhiên a để a²+3a +2 chia hết cho 6.

Giải:

Ta có a² +3a + 2 = (a+1)(a+2) là tích của 2 số tự nhiên liên tiếp nên chia hết cho 2

Do đó a² +3a +2 chia hết cho 3 ⇔ a² +2 chia hết cho 3

⇔ a² : 3 dư 1 ⇔ a không chia hết cho 3.

Điều kiện phải tìm là a không chia hết cho 3.

Bài 2:

Tìm điều kiện của số tự nhiên a để a⁴ -1 chia hết cho 240.

Bài 3:

Tìm số nguyên tố p để 4p +1 là số chính phương.

Bài 4.

Tìm ba số nguyên tố liên tiếp a,b,c sao cho a² + b² + c²  cũng là số nguyên tố

Giải: Xét hai trường hợp

+ Trong 3 số a,b,c có một số bằng 3.

Khi đó 2² + 3² + 5² =38 là hợp số (loại)

Còn 3² + 5² + 7² =83 là số nguyên tố.

+ Cả 3 số a,b,c đều lớn hơn 3.

Khi đó a², b², c² đều chia cho 3 dư 1 nên

a² + b² + c² chia hết cho 3,là hợp số (loại)

Vây ba số phải tìm là 3,5,7.

* Các bài tập tổng hợp các dạng toán trên

Bài 1. Cho bốn số nguyên dương a,b,c,d thảo mãn a² +b² = c² + d² .Chứng minh rằng a+ b+c+ d là hợp số.

Giải:

Xét biểu thức

A= (a² -a)+(b² -b)+( c² -c)+ (d² -d)

Dễ thấy A là số chẵn (vì biểu thức trong mỗi dấu ngoặc là tích của hai số nguyên liên tiếp) nên

(a² + b² + c² +d²) -(a+b + c+ d) là số chẵn

mà a² +b² = c² + d² nên a² +b² + c² + d²

là số chẵn.

Vậy a + b+ c + d là số chẵn,tổng này lớn hơn 2 nên là hợp số.

Bài 2. Cho các số nguyên a,b,c đều chia hết cho 6. Chứng minh rằng

Nếu a+ b+ c chia hết cho 6 thì a³ + b³  + c³

Chia hết cho 6

Giải:

Ta có  A=a³ + b³ + c³ – (a +b + c)

= (a³ -a) + (b³ -b) + (c³ -c)

Do a³ -a , (b³ -b) , (c³ -c) đều chia hết cho 6

Nên A $ displaystyle vdots $ 6

Mặt khác a+ b +c  chia hết cho 6

Do đó a³ +  b³  + c³  chia hết cho 6

Bài 3: Chứng minh rằng tổng các lập phương của ba sô nguyên liên tiếp thì  chia hết cho 9.

+ Hướng suy nghĩ: Tổng các lập phương của ba số nguyên liên tiếp có dạng như thế nào?

– HS: a³ + ( a + 1)³ + ( a + 2)³ hoặc  ( a -1)³ + a³ + ( a+ 1)³

+ Trong hai tổng vừa lập được hãy chọn tổng mà ta có thể biến đổi một cách nhẹ nhàng hơn

Bài 4: Chứng minh rằng A chia hết cho B với

A= 1³ + 2³ + 3³ +…+ 99 ³ + 100³

B= 1 + 2 + 3+…+ 99 + 100.

+ Hướng suy nghĩ cho hs: Bài toán trên thuộc dạng nào?

+  Trong hai tổng A và B ta tính được tổng nào? ( B = 50. 101)

+ Chứng tỏ A chia hết cho 5050? ( 1³ + 99³ $ displaystyle vdots $ 50. 101

Bài 5. Cho bốn số nguyên dương thoả mãn điều kiện ab = cd. Chứng minh rằng

a⁵ + b⁵ +c⁵ + d⁵ là hợp số

Giải:

Gọi ƯCLN (a,c) = k ( k nguyên dương)

Khi đó a = ka₁ , c= k .c₁ và ( a₁, c₁) =1

Thay vào a.b = c.d được

k.a₁ .b = k .c₁.d    nên a₁.b = c₁. d

ta có a₁.b c₁ mà ( a₁ , c₁)=1

nên b c₁ .Đặt b = c₁.m (m nguyên dương), thay vào (1) được

a₁.c₁.m = c₁.d nên a₁ .m = d

Do đó

A = a⁵ + b⁵ +c⁵ + d⁵

= k⁵ a₁⁵ + c₁⁵ m⁵ + c₁⁵ m⁵ +k⁵ c₁⁵ + a₁⁵ m⁵

= k⁵ ( a₁⁵ +c⁵) + m⁵ ( a⁵ + c⁵)

= (a₁⁵ + c₁⁵)( k⁵ + m⁵).

Do a₁, c₁ , k ,m là các số nguyên dương nên A là hợp số.

Bài 6. Chứng minh rằng nếu các số tự nhiên a,b,c thoả mãn điều kiện

a² + b² = c²  thì abc chia hết cho 60.

Giải: Theo bài ra  a² + b² = c²  (1)

Ta có  60 = 3. 4. 5

*Nếu a ,b ,c đều không chia hết cho 3 thì a², b² ,c² đều chia cho 3 dư 1.

Khi đó

a² + b² = Bs 3 + 2, còn c² = Bs 3 + 1 trái với (1).Vậy trong ba só a,b,c có một số chia hết cho 3.

*Nếu a,b,c đều không chia hết cho 5 thì a², b², c² chia cho 5 dư 1 hoặc 4. Khi đó a² +b² chia cho 5 dư 0,2,3 còn c² chia cho 5 dư 1,4 trái với (1).Vậy tồn tại một trong ba số a,b,c chia hết cho 5.

*Nếu a,b,c đều không chia hết cho 4 thì a², b², c² chia cho 8 dư 1 hoặc 4

Khi đó a² + b² chia cho 8 dư 0, 2 , 5, còn c² chia cho 8 dư 1, 4 trái với (1).Vậy tồn tại một số chia hết cho 4.

Kết luận: abc chia hết cho 3.4.5 tức là chia hết cho 60.