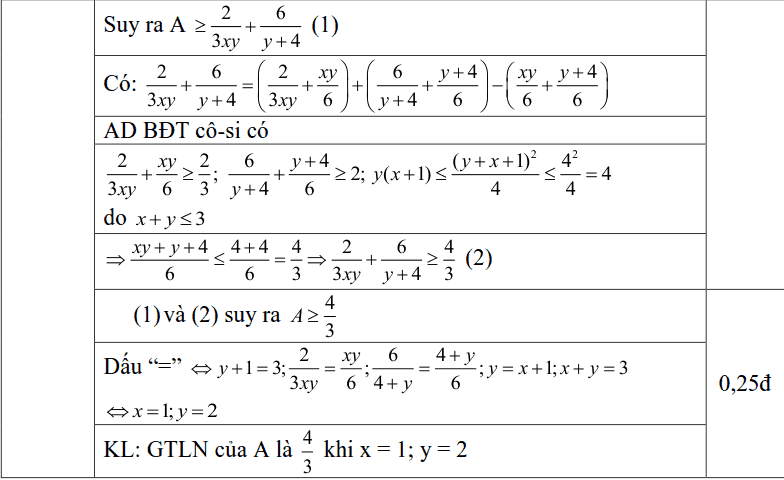Đề khảo sát học kì 2 môn Toán 9 phòng giáo dục và đào tạo quận Ba Đình năm học 2018-2019. Thời gian làm bài: 120 phút. Ngày khảo sát: 07/05/2019. Có đáp án.
Bài I (2,0 điểm). Cho hai biểu thức
A = $ frac{2}{{sqrt{x}-2}}$ và B = $ frac{{sqrt{x}}}{{x+1}}-frac{{4sqrt{x}+2}}{{xsqrt{x}-2x+sqrt{x}-2}}$ với $ xge 0;xne 4$
1) Tính giá trị của biểu thức A khi x = 16.
2) Rút gọn biểu thức P = A + B.
3) Tìm giá trị của x để biểu thức P đạt giá trị lớn nhất.
Bài II (2,0 điểm). Giải bài toán bằng cách lập phương trình hoặc hệ phương trình:
Một phòng họp có 300 ghế ngồi, được xếp thành một số hàng có số ghế bằng nhau. Buổi họp hôm đó có 378 người đến dự họp nên ban tổ chức đã kê thêm 3 hàng ghế và mỗi hàng ghế phải xếp thêm 1 ghế, mới đủ chỗ ngồi. Hỏi lúc đầu phòng họp có bao nhiêu hàng ghế và mỗi hàng ghế có bao nhiêu ghế, biết số hàng ghế ban đầu không vượt quá 20.
Bài III (2,0 điểm).
1) Giải hệ phương trình $ left{ begin{array}{l}frac{2}{{x-1}}+2sqrt{y}=8frac{{11}}{{x-1}}-3sqrt{y}=2end{array} right.$
a) Cho phương trình: $ {{x}^{2}}-(m-3)x-m+2=0$, (x là ẩn số)
b) Chứng minh rằng phương trình luôn có nghiệm với mọi giá trị của m.
2) Tìm m để phương trình có ít nhất một nghiệm dương.
Bài IV (0,5 điểm). Một hình cầu có thể tích là 288$ pi $(cm3). Tính diện tích mặt cầu đó.
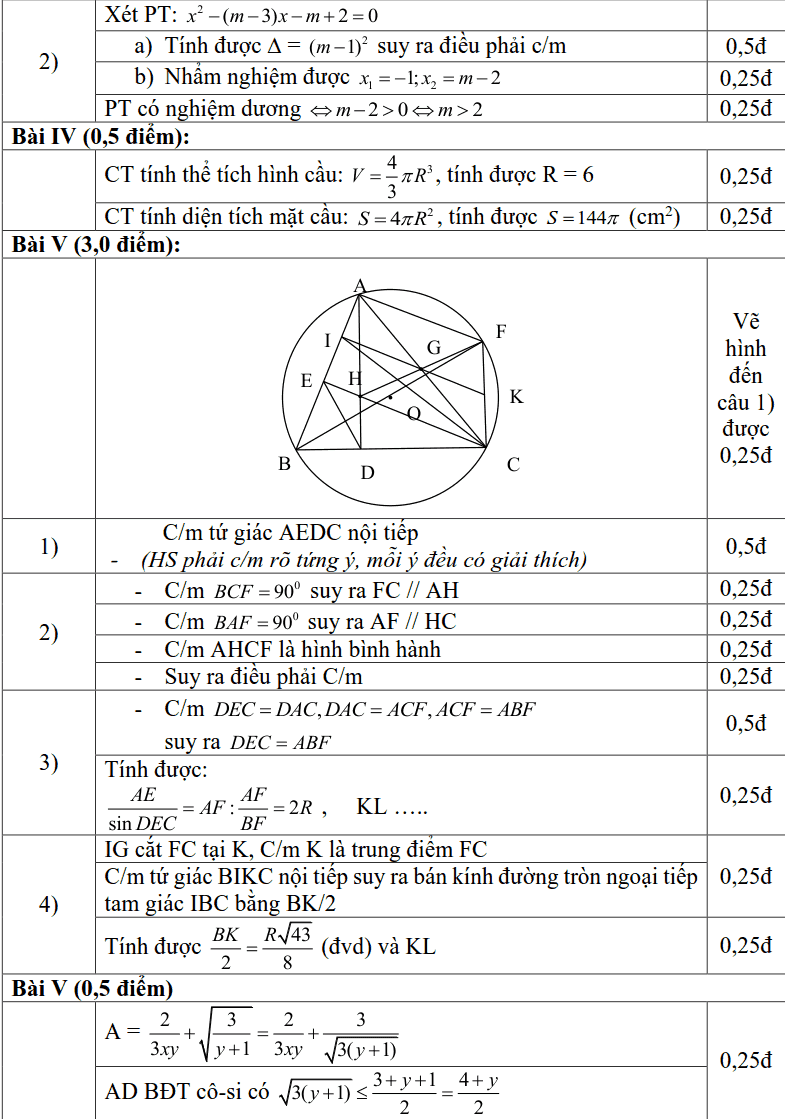
Bài V (3,0 điểm). Cho đường tròn (O;R) và dây BC cố định (BC < 2R), BF là đường kính. A là điểm di chuyển trên cung lớn BC (A khác B, C) sao cho tam giác ABC có ba góc nhọn, các đường cao AD và CE của tam giác ABC cắt nhau tại H.
1) Chứng minh tứ giác AEDC là tứ giác nội tiếp.
2) Chứng minh HF đi qua trung điểm G của đoạn thẳng AC.
3) Chứng minh $ displaystyle frac{{AF}}{{sin widehat{{DEC}}}}$ không đổi.
4) Cho BC = 1,5R; gọi I là hình chiếu của G trên AB. Hãy tính bán kính đường tròn ngoại tiếp tam giác IBC theo R.
Bài VI (0,5 điểm). Cho $ x,,,,y$ là các số thực dương thỏa mãn $ x+yle 3$. Tìm giá trị nhỏ nhất của biểu thức: A = $ frac{2}{{3xy}}+sqrt{{frac{3}{{y+1}}}}$
Hướng dẫn giải Đề khảo sát HK2 môn Toán 9 quận Ba Đình 2018-2019: