Đề kiểm tra giữa học kì 1 môn Toán lớp 8 trường THCS Thành Công, quận Ba Đình, năm học 2015 – 2016. Thời gian làm bài: 90 phút.
I. ĐẠI SỐ (10 điểm)
Bài 1 (2,5 điểm). Thu gọn các biểu thức sau:
a) $ 2yleft( {x+y} right)+3xleft( {x-y} right)+5$
b) $ left( {x+3} right)left( {2x-1} right)-3xleft( {x+2} right)left( {x-2} right)-{{left( {x-1} right)}^{3}}$
Bài 2 (3 điểm). Phân tích các đa thức sau thành nhân tử:
a) $ 4{{x}^{2}}y-2x{{y}^{2}}$
b) $ {{x}^{2}}-2xy+{{y}^{2}}-9$
c) $ left( {x+2} right)left( {{{x}^{2}}-2x} right)-3x-6$
Bài 3 (2 điểm). Tìm x, biết:
a) $ displaystyle 2xleft( {x-3} right)-3left( {3-x} right)=0$
b) $ {{x}^{3}}+5{{x}^{2}}-5=15x-32$
c) $ 8{{x}^{2}}+2x-15=0$
Bài 4 (1.5 điểm). Cho hai đa thức: $ Aleft( x right)=4{{x}^{4}}-11{{x}^{3}}+26{{x}^{2}}-43x+26$ và $ Bleft( x right)=4x-3$
a) Tính $ Aleft( x right):Bleft( x right)$
b) Tìm số nguyên x để $ Aleft( x right)$ chia hết cho $ Bleft( x right)$
Bài 5 (1 điểm).
a) Tìm giá trị nhỏ nhất của biểu thức $ A={{x}^{2}}+3x-5$
b) Chứng minh rằng $ Aleft( x right)=frac{1}{{120}}{{x}^{5}}-frac{1}{{24}}{{x}^{4}}+frac{1}{{14}}{{x}^{3}}+frac{1}{{24}}{{x}^{2}}-frac{1}{{20}}x$ nhận giá trị nguyên với mọi giá trị nguyên củ x.
II. PHẦN HÌNH HỌC (10 điểm)
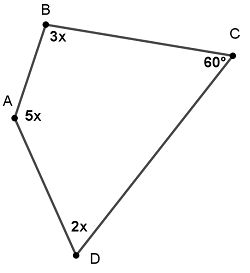
Bài 1 (5 điểm). Dùng lập luận để tìm x trong mỗi hình sau:
| Hình 1
|
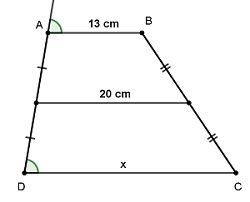
Hình 2
|
Bài 2 (5 điểm). Cho tam giác ABC. Qua trung điểm M của cạnh AB, kẻ MP song song với BC và MN song song với AC (P thuộc AC và N thuộc BC).
a) Chứng minh các tứ giác MNCP và BMPN là hình bình hành.
b) Gọi I là giao điểm của MN và BP, Q là giao điểm MC và PN. Chứng minh rằng: $ IQ=frac{1}{2}BC$ .
c) Tam giác ABC có điều kiện gì thì tứ giác BMPN là hình chữ nhật.