Đề kiểm tra khảo sát chất lượng môn Toán lớp 9 THCS Mỹ Đình 1, Phòng giáo dục và đào tạo quận Nam Từ Liêm, TP Hà Nội năm học 2018-2019.
Thời gian làm bài: 90 phút
Đề thi gồm 2 phần Trắc nghiệm và Tự luận.
PHẦN I. TRẮC NGHIỆM (1 điểm). Viết lại chữ cái đứng trước đáp án đúng trong các câu sau vào bài kiểm tra.
Câu 1. Biểu thức: $ sqrt{{3x-6}}$ xác định khi và chỉ khi:
A. $ xge 2$
B. $ xle 2$
C. $ xge -2$
D. $ xle -2$
Câu 2. Trục căn thức dưới mẫu của $ frac{{1+sqrt{2}}}{{3sqrt{2}}}$ ta được biểu diễn:
A. $ frac{{2+sqrt{2}}}{3}$
B. $ frac{{2+sqrt{2}}}{6}$
C. $ frac{{2-sqrt{2}}}{6}$
D. $ frac{{2+sqrt{2}}}{{18}}$
Câu 3. $ Delta ABC$ vuông tại A có AB = 2cm; AC = 4cm. Độ dài đường cao AH là:
A. $ frac{{2sqrt{5}}}{5}cm$
B. $ sqrt{5}cm$
C. $ frac{{4sqrt{5}}}{5}cm$
D. $ frac{{3sqrt{5}}}{5}cm$
Câu 4. Cho $ {{0}^{o}}<alpha <{{90}^{o}}$. Trong các đẳng thức sau, đẳng thức nào sai?
A. $ {{sin }^{2}}alpha +co{{s}^{2}}alpha =1$
B. $ tan alpha =cot ({{90}^{o}}-alpha )$
C. $ cot alpha =sin ({{90}^{o}}-alpha )$
D. $ tan alpha .cot alpha =1$
PHẦN II. TỰ LUẬN (9 điểm).
Bài 1 (2 điểm)
1. Thực hiện phép tính:
a) $ 4sqrt{{20}}-3sqrt{{125}}+5sqrt{{45}}-15sqrt{{frac{1}{5}}}$
b) $ frac{{3+sqrt{3}}}{{sqrt{3}}}-frac{2}{{sqrt{3}-1}}$
2. Giải phương trình: $ sqrt{{3x}}-2sqrt{{12x}}+frac{1}{3}sqrt{{27x}}=-4$
Bài 2 (2 điểm)
Cho hai biểu thức $ P=frac{{sqrt{x}-2}}{{sqrt{x}-3}}$ và $ Q=frac{{sqrt{x}}}{{sqrt{x}-3}}+frac{{6sqrt{x}}}{{9-x}}-frac{3}{{sqrt{x}+3}}$ với $ xge 0;xne 9$
a. Tính giá trị của P khi $ x=16$
b. Rút gọn Q
c. Tìm $ x$ để biểu thức A = P.Q có giá trị nhỏ nhất.
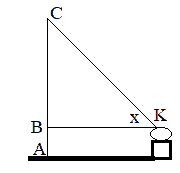
Bài 3 (1 điểm). Từ đài kiểm soát không lưu K, kỹ thuật viên đang kiểm soát một máy bay đang hạ cánh. Tại thời điểm này, máy bay đang ở độ cao 962 mét, góc quan sát (tính theo đơn vị độ, phút, giây) là $ {{26}^{o}}42’$. Hỏi máy bay tại thời điểm này cách đài quan sát bao nhiêu mét? Biết rằng đài quan sát cách mặt đất là 12 mét.
Bài 4 (3,5 điểm). Cho tam giác ABC có cạnh AB = 12cm, AC = 16cm, BC = 20cm. Kẻ đường cao AM. Gọi E là hình chiếu của M trên AB.
a) Chứng minh tam giác ABC là tam giác vuông.
b) Tính độ dài AM
c) Chứng minh $ AE.AB=A{{C}^{2}}-M{{C}^{2}}$
d) Chứng minh AE.AB = MB.MC = EM.AC
Bài 5 (0,5 điểm)
Với $ xge -frac{1}{2}$. Hãy tìm giá trị lớn nhất của biểu thức: $ A=sqrt{{2{{x}^{2}}+5x+2}}+2sqrt{{x+3}}-2x$
