Bài I. (3,0 điểm)
1. Giải hệ phương trình và phương trình sau:
a/ $ left{ begin{array}{l}2x-y=5x+y=4end{array} right.$ b/ $ 16{{x}^{4}}-8{{x}^{2}}+1=0$
2. Rút gọn biểu thức: $ A=frac{sqrt{{{left( sqrt{5}-1 right)}^{2}}}}{4}+frac{1}{sqrt{5}-1}$
3. Cho phương trình $ {{x}^{2}}-mx+m-1=0$ (có ẩn số x).
a/ Chứng minh phương trình đã cho luôn có hai nghiệm x1, x2 với mọi m.
b/ Cho biểu thức $ B=frac{2{{x}_{1}}{{x}_{2}}+3}{x_{1}^{2}+x_{2}^{2}+2left( 1+{{x}_{1}}{{x}_{2}} right)}$. Tìm giá trị của m để B = 1.
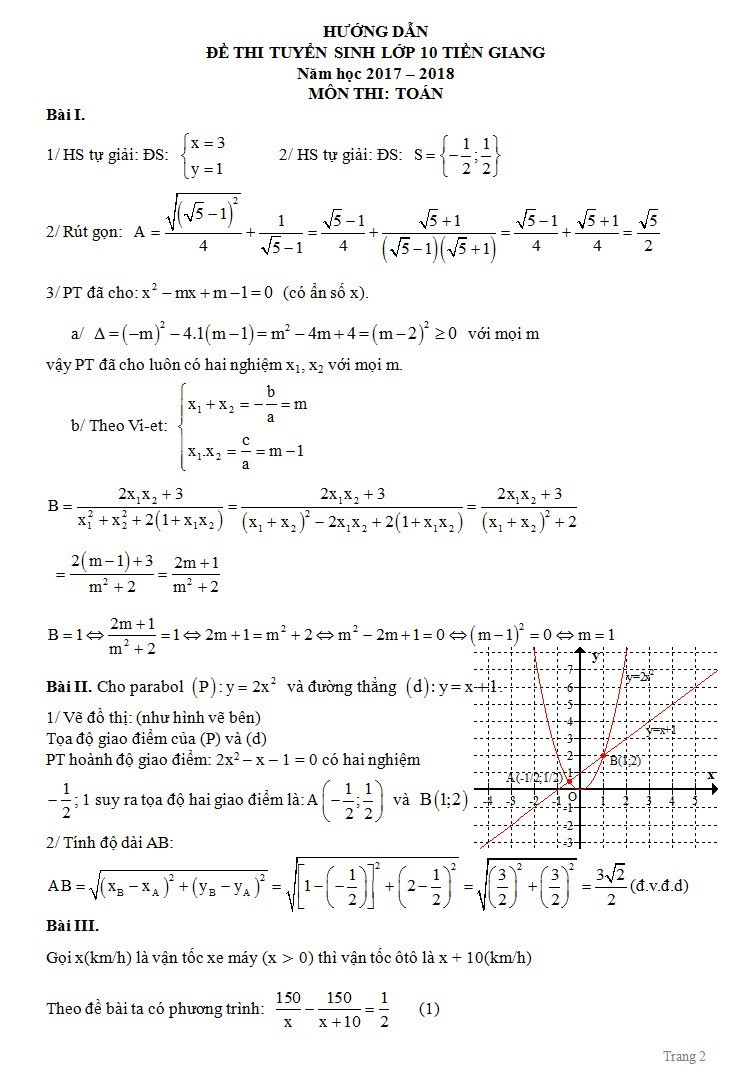
Bài II. (2,0 điểm) Cho parabol $ left( P right):y=2{{x}^{2}}$ và đường thẳng $ left( d right):y=x+1$.
1/ Vẽ đồ thị của (P) và (d) trên cùng hệ trục tọa độ.
2/ Bằng phép tính, xác định tọa độ giao điểm A và B của (P) và (d). Tính độ dài đoạn thẳng AB.
Bài III. (1,5 điểm) Hai thành phố A và B cách nhau 150km. Một xe máy khởi hành từ A đến B, cùng lúc đó một ôtô cũng khởi hành từ B đến A với vận tốc lớn hơn vận tốc của xe máy là 10km/h. Ôtô đến A được 30 phút thì xe máy cũng đến B. Tính vận tốc của mỗi xe.
Bài IV. (2,5 điểm) Cho nửa đường tròn tâm O, đường kính AB = 2R. Gọi M là điểm chính giữa của cung AB, N là điểm bất kỳ thuộc cung MB (N khác M và B). Tia AM và AN cắt tiếp tuyến tại B của nửa đường tròn tâm O lần lượt tại C và D.
1. Tính số đo $ widehat{ACB}$.
2. Chứng minh tứ giác MNDC nội tiếp trong một đường tròn.
3. Chứng minh AM.AC = AN.AD = 4R2.
Bài V. (1,0 điểm)
Cho hình nón có đường sinh bằng 26cm, diện tích xung quanh là $ 260pi $ cm2. Tính bán kính đáy và thể tích của hình nón.
HƯỚNG DẪN GIẢI: