Đề thi tuyển sinh vào lớp 10 môn Toán Sở giáo dục và đào tạo tỉnh Vĩnh Phúc năm học 2017 – 2018. Thời gian làm bài 120 phút (không kể thời gian giao đề).
Có 2 phần trắc nghiệm và tự luận.
I. TRẮC NGHIỆM (2,0 điểm). Trong 4 cái dưới đây mỗi câu có 4 lựa chọn, trong đó có duy nhất một lựa chọn đúng. Em hãy viết vào bài làm chữ cái A, B, C, D đứng trước lựa chọn em cho là đúng. (Ví dụ: Câu 1 nếu chọn A là đúng thì viết 1.A).
Câu 1: Giá trị của biểu thức $ sqrt{{{(3a-1)}^{2}}}$ là:
A. 3a-1 B. 1-3a C.3a-1 và 1-3a D. |3a – 1|
Câu 2: Hàm số $ y=(m+3)x+6$ đồng biến trên R, khi:
A. m > -3 B. m ≥ -3 C. m < -3 D. m ≤ -3
Câu 3: Đồ thị của hàm số nào sau đây đi qua hai điểm A(2;1), B(1;0):
A. y = x + 1 B. y = x – 1 C. y = -x + 1 D. y = -x – 1
Câu 4: Cho đường tròn (O;3cm) và đường thẳng a tiếp xúc với nhau tại điểm H. Khi đó:
A. OH > 3cm và OH vuông góc với a B. OH < 3cm và OH vuông góc với a
C. OH = 3cm và OH không vuông góc với a D. OH = 3cm và OH vuông góc với a
B. TỰ LUẬN (8.0 điểm)
Câu 5 ( 2.0 điểm) Cho hệ phương trình $ displaystyle left{ begin{array}{l}x-2y=3-m2x+y=3(m+2)end{array} right.,,,,,,(1),$ m là tham số.
a. Giải hệ (1) với m = 2.
b. Tìm tất cả các giá trị của m để hệ (1) có nghiệm duy nhất.
c. Tìm giá trị nhỏ nhất của biểu thức $ A={{x}^{2}}+{{y}^{2}}$, trong đó (x; y) là nghiệm duy nhất của hệ (1).
Câu 6 (2.0 điểm)
a. Một phòng họp có tổng số 80 ghế ngồi, được xếp thành từng hàng, mỗi hàng có số lượng ghế bằng nhau. Nếu bớt đi 2 hàng mà không làm thay đổi số lượng ghế tỏng phòng thì mỗi hàng còn lại xếp thêm 2 ghế. Hỏi lúc đầu trong phòng có bao nhiêu ghế?
b. Trên mặt phẳng tọa độ Oxy cho parabol $ (P):y={{x}^{2}}$ và đường thẳng $ (d):y=x-2$ cắt nhau tại hai điểm A, B. Tìm tọa độ các điểm A, B và tính diện tích tam giác AOB (trong đó O là gốc tọa độ, hoành độ của điểm A lớn hơn hoành độ điểm B).
Câu 7 (3,0 điểm)
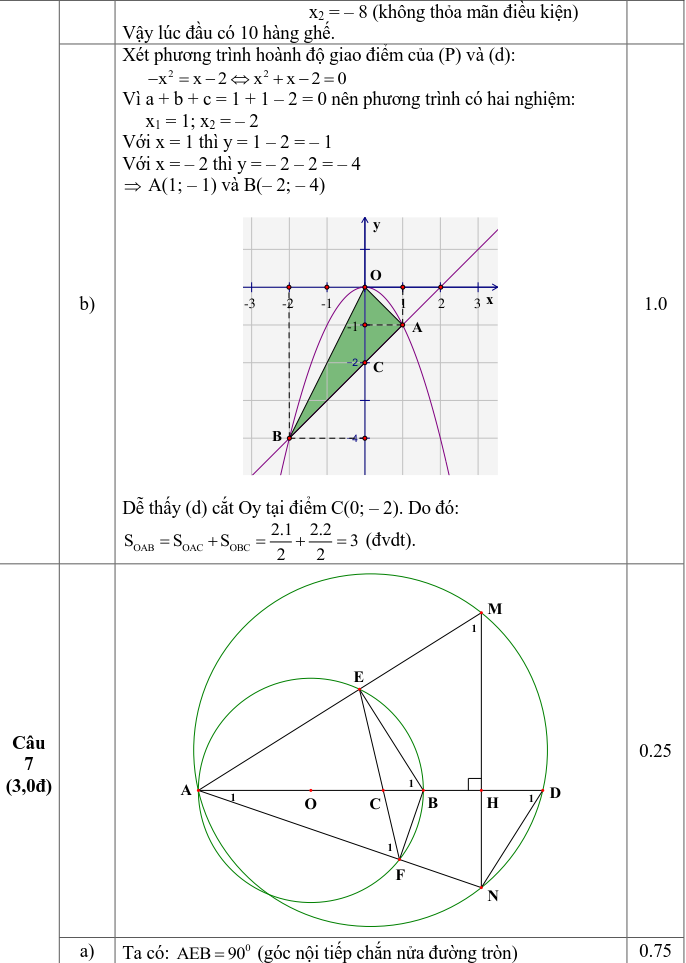
Cho đường tròn (O) có tâm là điểm O, đường kính AB = 2R. Trên đường thẳng AB lấy điểm H sao cho B nằm giữa A và H (H không trùng với B), qua H dựng đường thẳng d vuông góc với AB. Lấy điểm C cố định thuộc đoạn thẳng OB (C không trùng với O và B). Qua điểm C kẻ đường thẳng a bất kì cắt đường tròn (O) tại hai điểm E, F (a không trùng với AB). Các tia AE và AF cắt đường thẳng d lần lượt tại M và N.
a. Chứng minh rằng tứ giác BEMH nội tiếp đường tròn.
b. Chứng minh rằng tam giác AFB đồng dạng với tam giác AHN và đường tròn ngoại tiếp tam giác AMN luôn đi qua một điểm cố định khác A khi đường thẳng a thay đổi.
c. Cho AB = 4cm, BC = 1cm, HB = 1cm. Tìm giá trị nhỏ nhất của diện tích tam giác AMN.
Câu 12:(1,0 điểm)
Cho x, y là các số thực. Tìm giá trị lớn nhất của biểu thức:
$ P=frac{({{x}^{2}}-{{y}^{2}})(1-{{x}^{2}}{{y}^{2}})}{(1+{{x}^{2}})(1+{{y}^{2}})}$
HƯỚNG DẪN GIẢI VÀ BIỂU ĐIỂM DỰ KIẾN:
I. TRẮC NGHIỆM (2 điểm).
| Câu | 1 | 2 | 3 | 4 |
| Đáp án | D | A | B | D |
II. TỰ LUẬN (8 điểm).