Đề thi tuyển sinh vào lớp 10 môn Toán Khánh Hòa năm học 2014-2015
Thời gian làm bài: 120 phút (không kể thời gian giao đề)
Bài 1: (2 điểm)
1) Không dùng máy tính cầm tay, tính giá trị biểu thức: $ A=frac{1}{sqrt{2}+1}-frac{sqrt{8}-sqrt{10}}{2-sqrt{5}}$
2) Rút gọn biểu thức B = $ left( frac{a}{a-2sqrt{a}}+frac{a}{sqrt{a}-2} right):frac{sqrt{a}+1}{a-4sqrt{a}+4}$ với a > 0, a ≠ 4.
Bài 2: (2 điểm)
1) Cho hệ phương trình: $ displaystyle left{ begin{array}{l}ax-y=-yx-by=-aend{array} right.$
Tìm a và b biết hệ phương trình đã cho có nghiệm (x, y) = (2; 3).
2) Giải phương trình: 2(2x – 1) – $ displaystyle 3sqrt{5x-6}=sqrt{3x-8}$
Bài 3: (2 điểm)
Trong mặt phẳng Oxy cho parabol (P): $ y=frac{1}{2}{{x}^{2}}$
a) Vẽ đồ thị (P).
b)Trên (P) lấy điểm A có hoành độ xA = -2. Tìm tọa độ điểm M trên trục Ox sao cho |MA – MB| đạt giá trị lớn nhất, biết rằng B(1; 1).
Bài 4: (2 điểm)
Cho nửa đường tròn (O) đường kình AB = 2R. Vẽ đường thẳng d là tiếp tuyến của (O) tại B.
Trên cung $ oversetfrown{AB}$ lấy điểm M tùy ý (M khác A và B), tia AM cắt d tại N. Gọi C là trung điểm của AM, tia CO cắt d tại D.
a) Chứng minh rằng: OBNC nội tiếp.
b) Chứng minh rằng: NO ⊥ AD
c) Chứng minh rằng: CA. CN = CO . CD.
d) Xác định vị trí điểm M để (2AM + AN) đạt giá trị nhỏ nhất.
—– HẾT —–
Giám thị không giải thích gì thêm.
Gợi ý giải:
Bài 1: (2 điểm)
1) $ A=frac{1}{sqrt{2}+1}-frac{sqrt{8}-sqrt{10}}{2-sqrt{5}}=frac{sqrt{2}-1}{1}-frac{sqrt{2}(2-sqrt{5})}{2-sqrt{5}}=sqrt{2}-1-sqrt{2}=-1$
2) B = $ left( frac{a}{a-2sqrt{a}}+frac{a}{sqrt{a}-2} right):frac{sqrt{a}+1}{a-4sqrt{a}+4}$ với a > 0, a ≠ 4.
= $ left( frac{a}{a-2sqrt{a}}+frac{a}{sqrt{a}-2} right):frac{sqrt{a}+1}{a-4sqrt{a}+4}=left( frac{sqrt{a}}{sqrt{a}-2}+frac{a}{sqrt{a}-2} right)cdot frac{{{(sqrt{a}-2)}^{2}}}{sqrt{a}+1}$
= $ frac{sqrt{a}+a}{sqrt{a}-2}cdot frac{{{(sqrt{a}-2)}^{2}}}{sqrt{a}+1}=frac{sqrt{a}(1+sqrt{a})}{sqrt{a}-2}cdot frac{{{(sqrt{a}-2)}^{2}}}{sqrt{a}+1}=sqrt{a}(sqrt{a}-2)$
Bài 2: (2 điểm)
1) Vì hệ phương trình: $ displaystyle left{ begin{array}{l}ax-y=-yx-by=-aend{array} right.$ có nghiệm (x, y) = (2; 3) nên ta có hpt:
$ displaystyle left{ begin{array}{l}2a-3=-b2-3b=-aend{array} right.Leftrightarrow left{ begin{array}{l}2a+b=3a-3b=-2end{array} right.Leftrightarrow left{ begin{array}{l}6a+3b=9a-3b=-2end{array} right.Leftrightarrow left{ begin{array}{l}7a=72a+b=3end{array} right.Leftrightarrow left{ begin{array}{l}a=1b=1end{array} right.$
Vậy a = 1, b = 1
2) Giải phương trình: 2(2x – 1) – $ displaystyle 3sqrt{5x-6}=sqrt{3x-8}$
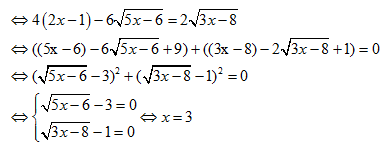
Vậy pt có nghiệm x = 3.
Bài 3: (2 điểm)
Trong mặt phẳng Oxy cho parabol (P):
a) Lập bảng giá trị (HS tự làm).
Đồ thị:
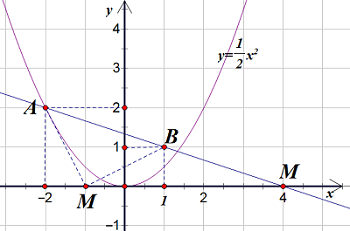
b) Vì A ∈ (P) có hoành độ xA = -2 nên yA = 2. Vậy A(-2; 2)
Lấy M(xM; 0) bất kì thuộc Ox,
Ta có: |MA – MB| ≤ AB (Do M thay đổi trên Ox và BĐT tam giác)
Dấu “=” xảy ra khi 3 điểm A, B, M thẳng hàng, khi đó M là giao điểm của đường thẳng AB và trục Ox.
– Lập pt đường thẳng AB
– Tìm giao điểm của đường thẳng AB và Ox, tìm M (4; 0).
Bài 4: (2,00 điểm)
Cho nửa đường tròn (O) đường kình AB = 2R. Vẽ đường thẳng d là tiếp tuyến của (O) tại B.
Trên cung $ oversetfrown{AB}$ lấy điểm M tùy ý (M khác A và B), tia AM cắt d tại N. Gọi C là trung điểm của AM , tia CO cắt d tại D.
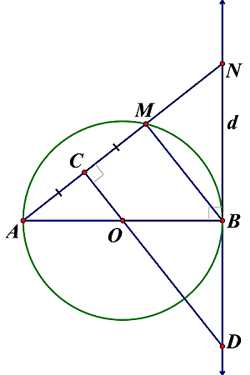
a) Chứng minh rằng: OBNC nội tiếp.
HD: Tứ giác OBNC nội tiếp có $ widehat{OCN}+widehat{OBN}={{180}^{0}}$
b) Chứng minh rằng: NO ⊥ AD
HD: ΔAND có hai đường cao cắt nhau tại O,
suy ra: NO là đường cao thứ ba hay: NO ⊥ AD
c) Chứng minh rằng: CA. CN = CO . CD.
HD: ΔCAO đồng dạng ΔCDN ⇒ $ frac{CA}{Ctext{D}}=frac{CO}{CN}$ ⇒ CA. CN = CO . CD
d) Xác định vị trí điểm M để (2AM + AN) đạt giá trị nhỏ nhất.
Ta có: 2AM + AN ≥ 2$ sqrt{2AM.AN}$ (BĐT Cauchy – Côsi)
Ta chứng minh: AM. AN = AB2 = 4R2. (1)
Suy ra: 2AM + AN ≥ 2$ sqrt{2.4{{R}^{2}}}$ = 4R$ sqrt{2}$
Đẳng thức xẩy ra khi: 2AM = AN Þ AM = AN/2 (2)
Từ (1) và (2) suy ra: AM = R$ sqrt{2}$ ⇒ ΔAOM vuông tại O ⇒ M là điểm chính giữa cung AB
