Đề thi tuyển sinh vào 10 môn Toán tỉnh Đồng Nai 2017 – 2018 có lời giải

Đề thi tuyển sinh môn Toán vào lớp 10 trung học phổ thông năm học 2017 – 2018 chuyên và không chuyên. Sở giáo dục và đào tạo Đồng Nai.  Có đáp án.

Thời gian làm bài 120 phút (không kể phát đề).

Đề thi không chuyên:

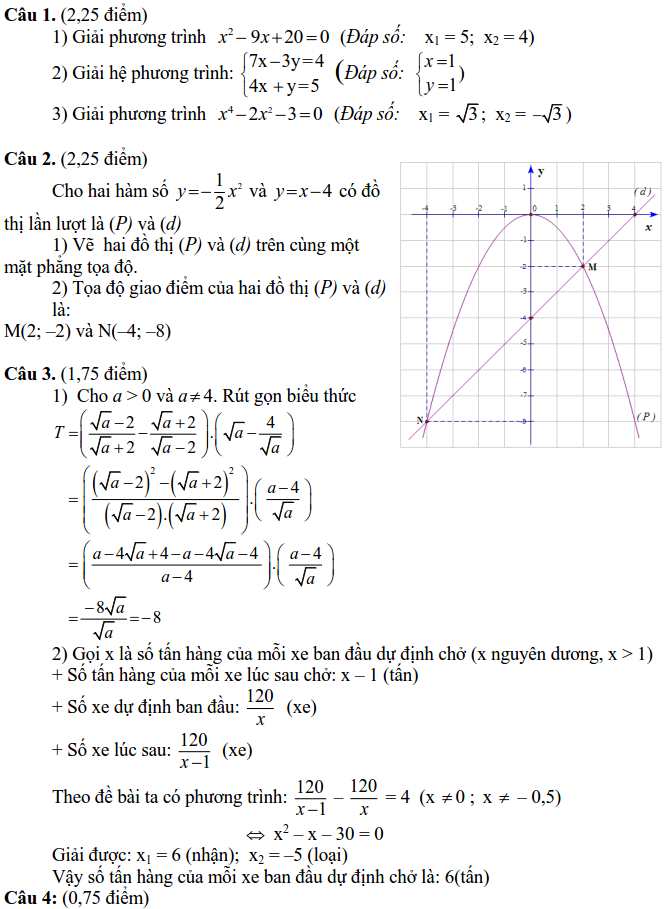
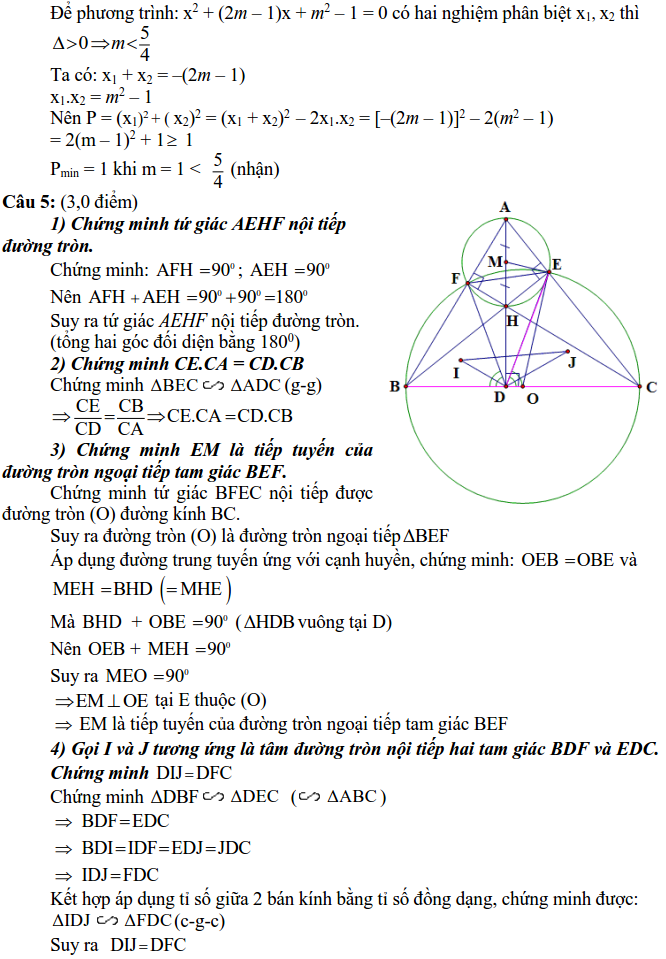
Hướng dẫn giải:

Đề thi vào lớp chuyên:

Bài 1:(1,75đ) Cho biểu thức : $ P=left( frac{a+sqrt{a}}{asqrt{a}+a+sqrt{a}+1}+frac{1}{a+1} right):left( frac{sqrt{a}-1}{a+1} right);(0le ane 1)$

1)Rút gọn P    ;

2)Tìm tất cả các số tự nhiên a để P có giá trị nguyên

Bài 2 : (2đ)

2.1) Giải phương trình : $ left( x+1 right)left( x+2 right)left( x+3 right)left( x+4 right)=24$

2.2) Giải hệ phương trình : $ left{ begin{array}{l}{{x}^{2}}-4xy+x+4y=2{{x}^{2}}-{{y}^{2}}=-3end{array} right.$

Bài 3: (1 đ) Gọi x₁ ; x₂ là hai nghiệm của phương trình x² – x – 5 = 0

Lập PT bậc hai có hai nghiệm là 2x₁ + x₂ và x₁ + 2x₂.

Bài 4: (1,5đ)

4.1)Giải phương trình nghiệm nguyên : $ {{x}^{2}}+2{{y}^{2}}-2xy-4x+8y+7=0$

4.2)Cho 3 số thực không âm a; b; c . Ch/m rằng:

$ ableft( {{b}^{2}}+bc+ca right)+bcleft( {{c}^{2}}+ac+ab right)+caleft( {{a}^{2}}+ab+bc right)le left( ab+bc+ca right)left( {{a}^{2}}+{{b}^{2}}+{{c}^{2}} right)$

Bài 5: Trong mặt phẳng tọa độ Oxy. Cho ngũ giác lồi ABCDE có các đỉnh có tọa độ nguyên. Chứng minh rằng : Tồn tại ít nhất một điểm M có toạ độ nguyên nằm trong ngũ giác hoặc trên các cạnh của ngũ giác đó ( không tính các đỉnh A,B,C,D,E)

Bài 6 : cho ABC nhọn . Đường trò (O) đường kính BC cắt AB, AC thứ tự tại M và N. Tia phân giác trong của các góc  : BAC , MON cắt nhau ở P

6.1)Chứng minh : $ widehat{OMN}=widehat{BAC}$ và tứ giác AMPN nội tiếp

6.2)Gọi Q là giao của các đường tròn ngoại tiếp các tam giác BMP & CNP.

Ch/m: ba điểm B, Q, C thẳng hàng

6.3)Gọi O1, O2, O3 thứ tự là tâm đường tròn ngoại tiếp các tam giác: AMN, BMP, CNP.

Ch/m: 4 điểm O, O1, O2, O3 cùng thuộc một đường tròn.

Đáp án: