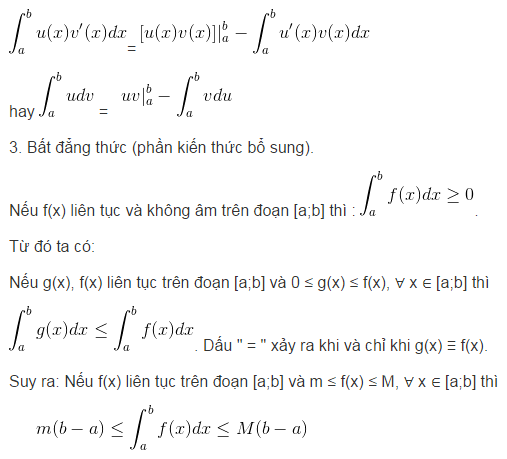Tiếp theo bài viết về lý thuyết nguyên hàm, ở bài này là lý thuyết tích phân bao gồm: định nghĩa, tính chất và phương pháp tính.
1. Định nghĩa tích phân
Cho hàm số f(x) liên tục trên đoạn [a;b]. Giả sử F(x) là một nguyên hàm của hàm số f(x) trên đoạn [a;b] , hiệu số F(b) – F(a) được gọi là tích phân từ a đến b (hay tích phân xác định trên đoạn [a;b] của hàm số f(x).
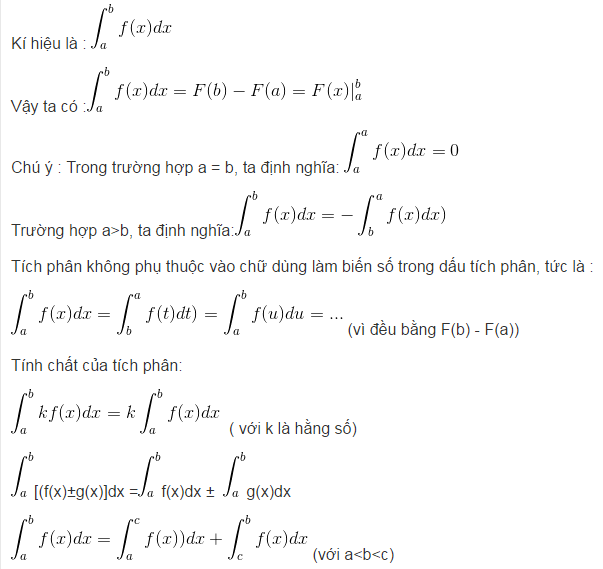
2. Phương pháp tính tích phân
a) Phương pháp đổi biến số
Định lí: Cho hàm số f(x) liên tục trên [a;b]. Giả sử hàm số x = φ(t) có đạo hàm liên tục trên đoạn [α;β] sao cho φ(α)=a, φ(β)=b và a ≤ φ(t) ≤ b , ∀t ∈ [α;β] . Khi đó:
Chú ý: Có thể dử dụng phép biến đổi số ở dạng sau:
Cho hàm số f(x) liên tục trên đoạn [a;b]. Giả sử hàm số u=u(x) có đạo hàm liên tục trên đoạn [a;b] sao cho α ≤ u(x) ≤ β, ∀ x∈ [a;b]. Nếu f(x) =g[u(x)].u’(x) ∀ x∈ [a;b], trong đó g(u) liên tục trên đoạn [α;β] thì:
b) Phương pháp tính tích phân từng phần
Định lí. Nếu u =u(x) và v=v(x) là hai hàm số có đạo hàm liên tục trên đoạn [a;b], thì: