1. Cho (O; R) tiếp tuyến của (O; R) là một đường thẳng tiếp xúc với (O; R).
2. Vậy d là tiếp tuyến (O; R) <=> d ⊥ OA tại A. A gọi là tiếp điểm.
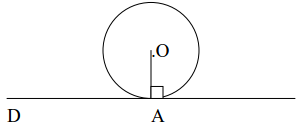
3. Nói cách khác : d là tiếp tuyến của (O; R) <=> d(O; d) =R.
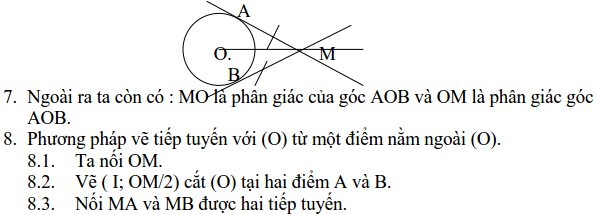
4. Ta có tính chất: từ một điểm M nằm ngoài (O; R) ta kẻ được hai tiếp tuyến đến (O; R) tại hai tiếp điểm A và B khi đó MA=MB.
5. Từ một điểm A trên (O; R) ta kẽ được một tiếp tuyến duy nhất, đó là đường thẳng qua A và vuông góc bán kính OA.
6. Từ hai điểm A và B trên (O) kẻ hai tiếp tuyến cắt nhau tại M thì MA= MB.
Bài tập:
1. Cho đường tròn tâm O; dây cung CD. Qua O vẽ OH CD tại H, cắt tiếp tuyến tại C của đường tròn tại M. C/m MD là tiếp tuyến của (O).
2. Cho (O) mà M ngoài (O). Vẽ hai tiếp tuyếm MA và MB; gọi H là giao điểm của OM với AB. C/m: OM ⊥ AB và HA=HB.
3. Cho nửa đường tròn tâm (O), đường kính AB vẽ Ax ⊥ AB và By ⊥ AB ở cùng phía nửa đường tròn. Gọi I là một điểm trên đường tròn. Tiếp tuyến tại I gặp Ax tại C và By tại D. C/m: AC+BD = CD.
4. Cho đường tròn (O; 5cm). Từ M ngoài (O) vẽ hai tiếp tuyến MA và MB sao cho MA ⊥ MB tại M.
a. Tính MA và MB.
b. Qua trung điểm I của cung nhỏ AB vẽ một tiếp tuyến cắt OA; OB tại C và D. Tính CD.
5. Cho (O) từ M ngoài (O) vẽ hai tiếp tuyến MA và MB sao cho góc AMB =600. Biết chu vi tam giác MAB là 18cm, tính độ dài dây cung AB.
6. Cho (O) từ M ngoài (O) vẽ hai tiếp tuyến MA và MB. Kéo dài OB một đoạn BI=OB. C/m: góc BMI bằng 1/3 góc AMI.
7. Cho (O) có đường kính AB. Vẽ dây cung AC bất kỳ và kéo dài AC một đoạn CD=AC.
a. C/m: tam giác ABD cân.
b. Xác định vị trí của C để biến đổi là tiếp tuyến của (O) tại B và tính góc DAB.
