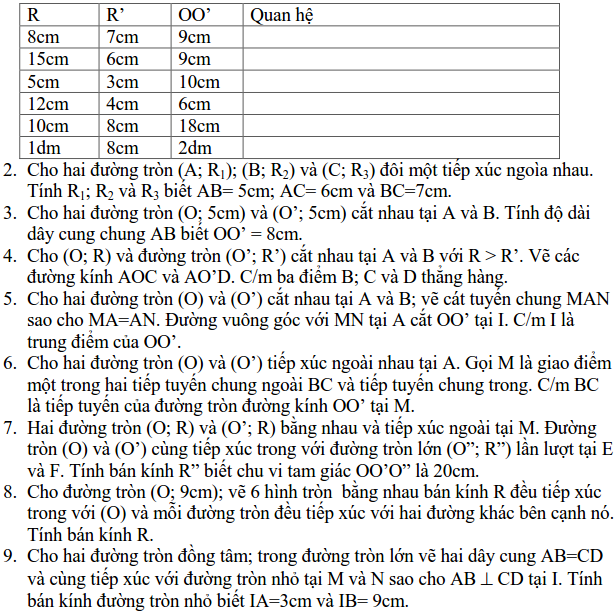
1. Cho hai đường tròn (O; R) và (O’; R’) khi đó dựa vào khoảng cách OO’ và R; R’ ta có các khả năng sau:
2. Nếu OO’ = R-R’ với R > R’ thì hai đường tròn này tiếp xúc trong.
3. Nếu OO’ = R +R’ thì hai đường tròn có một điểm chung và điểm này là giao điểm của OO’ và hai đường tròn. Ta gọi hai đường tròn tiếp xúc ngoài.
4. Nếu OO’ < R+R’ thì hai đường tròn này cắt nhau tại hai điểm. Hai điểm này nhận OO’ làm trung trực.
5. Nếu OO’ > R+R’ thì hai đường tròn không cắt nhau và ngoài nhau.
6. OO’ < R-R’ thì hai đường tròn đựng nhau. (O; R) chứa (O’; R’) hay (O’; R) chứa trong (O; R).
7. Hai đường tròn đồng tâm là hai đường tròn có cùng tâm.
8. Nếu có hai đường tròn thì tiếp tuyến chung của chúng và đường nối tâm OO’ đồng quy.
– Nếu đồng quy bên trong đoạn OO’ thì gọi là tiếp tuyến chung trong.
– Nếu đồng quy bên ngoài đoạn OO’ thì gọi là tiếp tuyến chung ngoài.
– Điếm đồng quy này chia OO’ theo tỉ lệ bằng tỉ lệ hai bán kính.
Bài tập:
1. Hãy điền vào bảng sau vị trí giữa (O; R) và (O’; R’) biết: