Để làm được bài tập về số nguyên tố và hợp số các em học sinh cần phải nắm được lý thuyết và sau đó làm theo các ví dụ mẫu.
Lý thuyết và số nguyên số và hợp số các em chỉ cần đọc lại ở bài viết này: https://Toancap2.net/so-nguyen-to-hop-so-bang-so-nguyen-to/
Tiếp theo là các dạng bài tập về Số nguyên tố và Hợp số – Số học 6.
Dạng 1: Nhận biết số nguyên tố, hợp số
Phương pháp giải
Căn cứ vào định nghĩa số nguyên tố và hợp số.
Căn cứ vào các dấu hiệu chia hết.
Có thể dùng bảng số nguyên tố ở cuối Sgk để xác định một số (nhỏ hơn 1000) là số nguyên tố hay không.
Dạng 2: Viết số nguyên tố hoặc hợp số từ những số cho trước
Phương pháp giải
Dùng các dấu hiệu chia hết
Dùng bảng số nguyên tố nhỏ hơn 1000.
Dạng 3: Chứng minh một số là số nguyên tố hay hợp số
Phương pháp giải
Để chứng minh một số là số nguyên tố, ta chứng minh số đó không có ước nào khác 1 và chính nó.
Để chững minh một số là hợp số, ta chỉ ra rằng tồn tại một ước của nó khác 1 và khác chính nó. Nói cách khác, ta chứng minh số đó có nhiều hơn hai ước.
VD: Cho m2 +2 và m là hai số nguyên tố, chứng minh m3+2 cũng là số nguyên tố HD: m=2 (loại), m=3 ™, m=3k+1 loại, m=3k+2 loại, KL: m=3
VD: cho p và 8p2+1 là số nguyên tố .CMR 8p2-1 cũng là số nguyên tố.
Dạng 4: Phân tích các số cho trước ra thừa số nguyên tố
Phương pháp giải:
Thường có hai cách phân tích một số tự nhiên n (n >1) ra thừa số nguyên tố.
– Cách làm (phân tích theo cột dọc ): Chia số n cho một số nguyên tố (xét từ nhỏ đến lớn ), rồi chia thương tìm được cho một số nguyên tố (cũng xét từ nhỏ đến lớn), cứ tiếp tục như vậy cho đến khi thương bằng 1.
Ví dụ: Phân tích số 90 ra thừa số nguyên tố
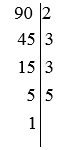
Khi đó ta được: 90 = 2.32.5
*Bài tập rèn luyện:
Bài 1: Tổng (hiệu) sau là số nguyên tố hay hợp số:
a) 3150 + 2125
b) 5163 + 2532
c) 19. 21. 23 + 21. 25 .27
d) 15. 19. 37 – 225
Hướng dẫn
Tổng lớn hơn 5 và chia hết cho 5, nên tổng là hợp số.
Hiệu lớn hơn 3 và chia hết cho 3, nên hiệu là hợp số.
Tổng lớn hơn 21 và chia hết cho 21 nên tổng là hợp số.
Hiệu lớn hơn 15 và chia hết cho 15 nên hiệu là hợp số.
Bài 2: Chứng tỏ rằng các số sau đây là hợp số:
a) 297; 39743; 987624
b) 111…1 có 2001 chữ số 1 hoặc 2007 chữ số 1
Các số trên đều chia hết cho 11
Dùng dấu hiệu chia hết cho 11 đê nhận biết: Nếu một số tự nhiên có tổng các chữ số đứng ở vị trí hàng chẵn bằng tổng các chữ số ở hàng lẻ ( số thứ tự được tính từ trái qua phải, số đầu tiên là số lẻ) thì số đó chia hết cho 11. Chẳng hạn 561, 2574,…
Nếu số đó có 2001 chữ số 1 thì tổng các chữ số của nó bằng 2001 chia hết cho 3. Vậy
số đó chia hết cho 3. Tương tự nếu số đó có 2007 chữ số 1 thì số đó cũng chia hết cho 9.
Bài 3: Tổng hiệu sau là số nguyên tố hay hợp số
a) A = 15.17 + 91.
b) B = 2.3.5.7.11+13.17.19.21.
c) C = 3 + 3.41+ 240
d) D = 45 + 36 + 72 + 81
e) E =13 – 29.13 +12.13
g) G = 4.19 – 5.4
h) H = 32 + 3.17 + 34.33
i) I = 7 + 72 + 73 + 74 + 75
Bài 4: Chứng minh rằng các tổng sau đây là hợp số
abcabc + 7
abcabc + 22
abcabc + 39
