Phương pháp giải toán hình học trên tọa độ Oxy lớp 10

Bài toán 1 : Cho tam giác ABC có A(1; 5), B (-3;1) và C(5;1)

a) Tính chu vi, tam giác ABC là tam giác gì ?

b) Tính diện tích và bán kính đường tròn nội tiếp của tam giác ABC.

GIẢI.

Độ dài các cạnh :

$AB=sqrt{(-3-1)^2 (1-5)^2}=4sqrt{2}$

$AC=sqrt{(5-1)^2 (1-5)^2}=4sqrt{2}$

$BC=sqrt{(5 3)^2 (1-1)^2}=8$

chu vi : C = AB AC BC = $4sqrt{2} 4sqrt{2} 8=8sqrt{2} 8$
ta có : $AB=AC=4sqrt{2}$ => tam giác ABC cân tại A

AB² AC² = 32 32 = 64

BC² = 8²=64

=> BC² = AB² AC²
=> tam giác ABC vuông tại A
Vậy : tam giác ABC vuông cân tại A
b) diện tích : S = AB.AC/2 = $4sqrt{2}.4sqrt{2}$ /2 = 16 (đvdt)
nữa chu vi : p =( $4sqrt{2} 4sqrt{2} 8$ )/2 = $4sqrt{2} 4$
ta có : S =pr => r = S/p = 16/( $4sqrt{2} 4$ ) = $4(sqrt{2}-1)$

Bài toán 2 : Trong mp tọa độ Oxy, cho A(5;1), B(1;-1), C(3;3) .

a) tìm tọa độ điểm D sao cho tứ giác ABCD là hình bình hành.

b) tìm tọa độ điểm M biết : ⇔ $overrightarrow {AM}=3overrightarrow {BC}-2overrightarrow {CA}$

GIẢI.

a) gọi tọa độ điểm D(x; y)
tứ giác ABCD là hình bình hành khi : $overrightarrow {AD}=overrightarrow {BC}$
ta có : $overrightarrow {AD}=(x-5 ;y-1)$
$overrightarrow {BC}=(3-1;3 1)=(2;4)$
Nên :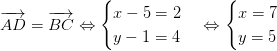
Vậy : D(7; 5)
b) gọi tọa độ điểm M(x; y)
ta có : $overrightarrow {AM}=(x-5 ;y-1)$

$overrightarrow {BC}=(3-1;3 1)=(2;4)$

$overrightarrow {CA}=(5-3;1-3)=(2;-2)$

$overrightarrow {AM}=3overrightarrow {BC}-2overrightarrow {CA}$

(x – 5; y – 1 ) =3(2; 4) – 2(2; -2) = (2; 16)

=> x – 5 = 2 và y – 1 = 16

x = 7 và y = 17

vậy : M(7; 17)

Bài toán 3 : Trong mp tọa độ Oxy, cho A(5;8), B(-2;1), C(4;3) .

a) Tìm tọa độ điểm M thuộc trục tung để ba điểm B, M, A thẳng hàng

b) Tìm tọa độ điểm N trên Ox để tam giác ABN cân tại N

GIẢI.

a) Gọi tọa độ điểm M thuộc trục tung : M(0; y)

Ta có :
$overrightarrow {AB}=(-2-5 ;1-8)=(-7;-7)$
$overrightarrow {AM}=(0-5;y-8)= (-5;y-8)$
để ba điểm A, M, B, thẳng hàng khi $overrightarrow {AB},overrightarrow {AM}$ cùng phương. Nên ta có :

-5/-7 = (y-8)/-7

<=> y – 8 = -5

<=> y = 3

Vậy : M(0; 3) thì A, M, B, thẳng hàng.
b) Gọi tọa độ điểm N thuộc trục hoành : N(x; 0)
để tam giác ABN cân tại N khi : AN = BN

<=> AN² = BN²

<=> (x – 5)² (-8)² = (x 2)² (-1)²

<=> x² – 10x 25 64 = x² 4x 4 1

<=> 14x = 84

<=> x = 6

vậy : N(6; 0) thì tam giác ABN cân tại N.

Bài toán 4: Tìm trực tâm của tam giác ứng dụng tích vô hướng :

Trong mp tọa độ Oxy, cho A(5;1), B(1;-1), C(3;3) .

Tìm tọa độ trực tâm H của tam giác ABC.
Tính độ dài đường cao kẻ từ A của tam giác ABC.

GIẢI.

1) Gọi tọa độ điểm H : H(x; y)
Ta có :

$overrightarrow {BC}=(3-1;3 1)=(2;4)$

$overrightarrow {AC}=(3-5;3-1)=(-2;2)$

$overrightarrow {AH}=(x-5;y-1)$

$overrightarrow {BH}=(x-1;y 1)$

Do trực tâm H của tam giác ABC. Nên : AH vuông góc BC và BH vuông góc AC :

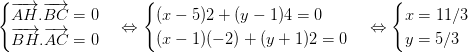
Vậy : H(11/3 ; 5/3)
2. gọi tọa độ điểm D(x; y).
$overrightarrow {AD}=(x-5;y-1)$
AD vuông góc BC, nên : $overrightarrow {AD}.overrightarrow {BC}=0$

2(x-5) 4(y-1) =0 <=> x 2y – 7 = 0 (1)

$overrightarrow {BD}=(x-1;y 1)$
Do B; D; C thẳng hàng, nên : $overrightarrow {BD},overrightarrow {BC}$ cùng phương. Nên ta có :

(x-1)/2 = (y 1)/4 <=> 2x – 2 = y 1 <=> 2x – y – 3 = 0 (2)

Từ (1) và (2), ta có hệ :

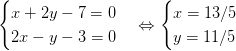
Vậy : D(13/5; 11/5)

Bài toán 5: Tâm I đường tròn ngoại tiếp tam giác ứng dụng tích vô hướng :

Cho tam giác ABC có A(-1;1); B(1;3); C(1;-1)
Tìm tọa độ tâm I đường tròn ngoại tiếp tam giác ABC

GIẢI.

Tọa độ trung điểm M của AB :
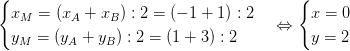=> M(0; 2)
Tọa độ trung điểm N của AC :
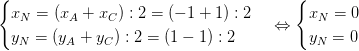=> N(0; 0)
gọi tọa độ điểm I(x; y). A(-1;1); B(1;3); C(1;-1)
$overrightarrow {MI}=(x;y-2)$
$overrightarrow {NI}=(x;y)$
$overrightarrow {AB}=(1-1;3-1)=(0;2)$
$overrightarrow {AC}=(1 1;-1-1)=(2;-2)$
tâm I đường tròn ngoại tiếp tam giác ABC, nên :
MI vuông góc AB và NI vuông góc AC :

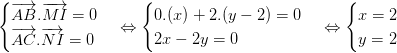
Vậy : tâm I(2; 2) đường tròn ngoại tiếp tam giác ABC.