Lý thuyết Tổng và hiệu của hai vectơ
Lý thuyết vectơ dưới đây.
1. Tổng của hai vectơ
Cho hai vectơ $ displaystyle overrightarrow{a}$, $ displaystyle overrightarrow{b}$ . Lấy một điểm A tùy ý, vẽ $ displaystyle overrightarrow{AB}=overrightarrow{a}$ , $ displaystyle overrightarrow{AB}=overrightarrow{b}$ . Vectơ $ displaystyle overrightarrow{AC}$ được gọi là tổng của hai vectơ $ displaystyle overrightarrow{a}$ và $ displaystyle overrightarrow{b}$ .
$ displaystyle overrightarrow{AC}=overrightarrow{a} overrightarrow{b}$
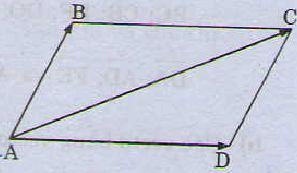
2. Quy tắc hình bình hành
Nếu ABCD là hình bình hành thì:
$ displaystyle overrightarrow{AB} overrightarrow{AD}=overrightarrow{AC}$
3. Tính chất của tổng các vectơ
– Tính chất giao hoán: $ displaystyle overrightarrow{a} overrightarrow{b}=overrightarrow{b} overrightarrow{a}$
– Tính chất kết hợp: $ displaystyle (overrightarrow{a} overrightarrow{b}) overrightarrow{c}=overrightarrow{a} (overrightarrow{b} overrightarrow{c})$
– Tính chất của $ displaystyle overrightarrow{0}$ : $ displaystyle overrightarrow{a} overrightarrow{0}=overrightarrow{0} overrightarrow{a}$
4. Hiệu của hai vectơ
a) Vec tơ đối: Vectơ có cùng độ dài và ngược hướng với vetơ $ displaystyle overrightarrow{a}$
được gọi là vec tơ đối của vectơ $ displaystyle overrightarrow{a}$ , kí hiệu là $ displaystyle -overrightarrow{a}$ .
Vectơ đối của $ displaystyle overrightarrow{0}$ là vectơ $ displaystyle overrightarrow{0}$
b) Hiệu của hai vectơ: Cho hai vectơ $ displaystyle overrightarrow{a}$, $ displaystyle overrightarrow{b}$ . Vectơ hiệu của hai vectơ, kí hiệu $ displaystyle overrightarrow{a}-overrightarrow{b}$ là vectơ $ displaystyle overrightarrow{a} (-overrightarrow{b})$ :
$ displaystyle overrightarrow{a}-overrightarrow{b}$ = $ displaystyle overrightarrow{a} (-overrightarrow{b})$
c) Chú ý: Với ba điểm bất kì, ta luôn có
$ displaystyle overrightarrow{AB} overrightarrow{BC}=overrightarrow{AC}$ (1)
$ displaystyle overrightarrow{AB}-overrightarrow{AC}=overrightarrow{CB}$ (2)
(1) là quy tắc 3 điểm (quy tắc tam giác) đối với tổng của hai vectơ.
(2) là quy tắc 3 điểm (quy tắc tam giác) đối với hiệu các vectơ.
5. Áp dụng
a) Trung điểm của đoạn thẳng:
I là trung điểm của đoạn thẳng ⇔ $ displaystyle overrightarrow{IA} overrightarrow{IB}=overrightarrow{0}$
b) Trọng tâm của tam giác:
G là trọng tâm của tam giác ∆ABC ⇔ $ displaystyle overrightarrow{GA} overrightarrow{GB} overrightarrow{GC}=overrightarrow{0}$
