Hướng dẫn sử dụng lý thuyết ứng dụng của tích phân trong hình học bao gồm: tính diện tích hình phẳng, thể tích vật thể, thể tích khối tròn xoay.
Các phương pháp tính diện tích, thể tích bằng tích phân:
1. Tính diện tích hình phẳng
a) Nếu hình phẳng được giới hạn bởi đồ thị hàm số y = f(x) liên tục t trên đoạn [a;b]; trục hoành và hai đường thẳng x = a; x = b (h.1), thì diện tích S được cho bởi công thức:
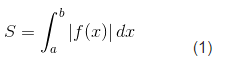
Chú ý : Để tính tích phân trên, ta xét dấu của f(x) trên đoạn [a,b]. Nếu f(x) không đổi dấu
trên khoảng (c;d) ⊂ [a;b] thì:

Bước 3: Tính diện tích theo công thức (*):

2. Tính thể tích vật thể
Một vật thể được giới hạn bởi hai mặt phẳng vuông góc với trục hoành tại điểm có hoành độ
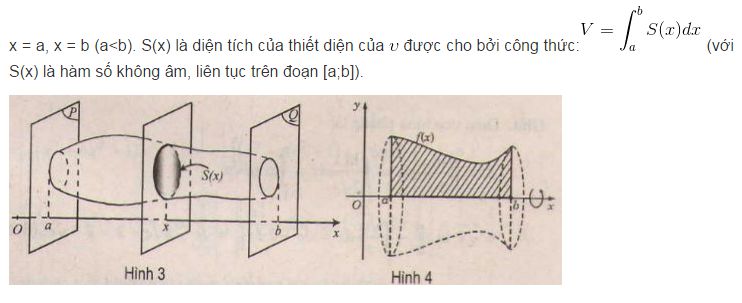
3. Tính thể tích khối tròn xoay
a) Hình phẳng quay quanh trục Ox: Cho hình phẳng được giới hạn bởi đồ thị hàm sốy = f(x) không âm và liên tục trên đoạn [a;b], trục Ox và hai đường thẳng x = a, x = b quay quanh trục Ox, ta được khối tròn xoay (h.4). Thể tích Vx của khối tròn xoay này được cho bởi công thức:
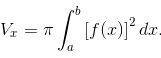
b) Hình phẳng quay quanh trục Oy (kiến thức bổ sung): Cho hình phẳng được giới hạn bởi đồ thị hàm số x = g(y) không âm và liên tục trên đoạn [c;d], trục Oy và hai đường thẳng y = c, y = d quay quanh trục Oy, ta được khối tròn xoay. Thể tích Vy của khối tròn xoay này được cho bởi công thức:

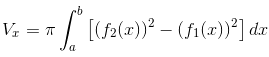
Tương tự, đổi vai trò x và y cho nhau, ta có công thức tính Vy (khi hình phẳng quay quanh trục Oy).
