A. LÝ THUYẾT
1. Đường trung bình của tam giác
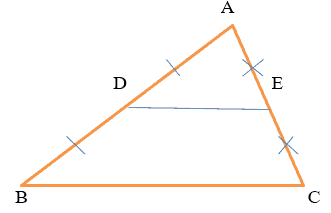
Định nghĩa : Đường trung bình của tam giác là đoạn thẳng nối trung điểm của hai cạnh của tam giác.
Định lý 1.
| Đường thẳng đi qua trung điểm của một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm của cạnh thứ ba. |
Định lý 2.
| Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy. |
2. Cách chứng minh đoạn thẳng là đường trung bình của tam giác
Có 2 cách : (hình minh họa ở trên)
Cách 1 : Chứng minh D là trung điểm của AB và E là trung điểm của AC à DE là đường trung bình của tam giác ABC.
Cách 2 : Chứng minh D là trung điểm của AB và DE song song với BC à DE là đường trung bình của tam giác ABC.
3. Đường trung bình của hình thang
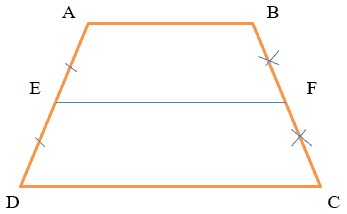
Định nghĩa : Đường trung bình của hình thang là đoạn thẳng nối trung điểm của hai cạnh bên của hình thang.
Định lý 3.
| Đường thẳng đi trung điểm một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm cạnh bên thứ hai. |
Định lý 4.
| Đường trung bình của hình thang thì song song với hai cạnh đáy và bằng nửa tổng hai đáy. |
4. Cách chứng minh đoạn thẳng là đường trung bình của hình thang
Có 2 cách chứng minh.
Cách 1 : Chứng minh E là trung điểm của AD và F là trung điểm của BC à EF là đường trung bình của hình thang ABCD.
Cách 2 : Chứng minh E là trung điểm của AD và EF // DC à EF là đường trung bình của hình thang ABCD.
B. BÀI TẬP
Bài toán 1 : Cho tứ giác ABCD. Gọi E, F, K theo thứ tự là trung điểm của AD, BC, AC.
a) So sánh độ dài EK và CD, KF và AB.
b) Chứng minh rằng EF $ displaystyle le $ $ displaystyle frac{{AB+CD}}{2}$
Gợi ý :
– Học sinh tự vẽ hình.
– a) dựa vào tính chất đường trung bình trong tam giác.
– b) dựa vào ý a) đã chứng minh + bất đẳng thức trong tam giác.
Bài toán 2 : Cho tứ giác ABCD. Gọi E, F, I theo thứ tự là trung điểm của AD, BC, AC.
Chứng minh rằng :
a) EI // CD, IF // AB.
b) EF $ displaystyle le $ $ displaystyle frac{{AB+CD}}{2}$
Gợi ý : tương tự bài toán 1.
Bài toán 3 : Cho hình thang ABCD có đáy AB, CD. Gọi E, F, I theo thứ tự là trung điểm của AD, BC, AC. Chứng minh rằng ba điểm E, I, F thẳng hàng.
Gợi ý :
– Học sinh tự vẽ hình.
– chứng minh EI // DC và FI // DC suy ra EI trùng FI suy ra ba điểm thẳng hàng.
Bài toán 4 : Cho tam giác ABC, các trung tuyến BE và CD cắt nhau tại G. Gọi I, K theo thứ tự là trung điểm của GB, GC. Chứng minh rằng DE song song và bằng IK.
Gợi ý :
– Học sinh tự vẽ hình.
– Dựa vào dữ kiện đề bài cho + đường trung bình trong tam giác.
Bài toán 5 : Cho tam giác ABC, điểm D thuộc cạnh AC sao cho AD = $ displaystyle frac{1}{2}$DC. Gọi M là trung điểm của BC, I là giao điểm của BD và AM. Chứng minh rằng AI = IM.
Gợi ý :
– Học sinh tự vẽ hình.
– Gọi O là trung điểm của DC. Đi chứng minh MO // DI. Chứng minh tiếp DI là đường trung bình của tam giác AMO.
Bài toán 6 : Cho tam giác ABC, đường trung tuyến AM. Gọi D là trung điểm của AM, E là giao điểm của BD và AC. Chứng minh rằng AE = $ displaystyle frac{1}{2}$EC.
Gợi ý :
– Học sinh tự vẽ hình.
– Gọi N là trung điểm của EC rồi chưng minh MN // ED.
– Chứng minh DE là đường trung bình của tam giác AMN.
Bài toán 7 : Cho tam giác ABC. Vẽ đường cao AH. Gọi D, E theo thứ tự là trung điểm của các cạnh AB và AC. Vẽ DI và EK cùng vuông góc với BC. Chứng minh rằng :
a) DI = EK.
b) IK = $ displaystyle frac{1}{2}$
Gợi ý :
– Học sinh tự vẽ hình minh họa.
– dựa vào đường trung bình chứng minh DI = 1/2 AH và EK = 1/2AH.
– I là trung điểm của BH, và K là trung điểm của HC. Dựa vào đó để chứng minh.
Bài toán 8 : Cho tam giác ABC. Điểm D, E thuộc cạnh AB sao cho AD = DE = EB. Vẽ DG và EF song song với BC.
a) Chứng minh rằng AG = GF = FC.
b) Cho DG = 5cm. Tính BC.
Gợi ý :
– Học sinh tự vẽ hình.
– a) Dựa vào đường trung bình trong tam giác.
Bài toán 9 : Cho hình thang ABCD (AB// CD). gọi E, F, I, K theo thứ tự là trung điểm của AD, BC, AC, BD. Tính độ dài các đoạn thẳng EK, KI, IF biết AB = 18cm và CD = 12cm.
Gợi ý : Dựa vào tính chất đường trung bình trong tam giác và hình thang.
Bài toán 10 : Cho hình thang vuông ABCD (A = D = 90o). Gọi M là trung điểm của BC. Chứng minh rằng tam giác MAD là tam giác cân.
Gợi ý :
– Cách 1 : Gọi N là trung điểm của AD, chứng minh MN vuông góc với AD. Suy ra tam giác có MN vừa là đường cao vừa là đường trung tuyến nên là tam giác cân.
– Cách 2 : gọi E là giao điểm của AM và DC. $ displaystyle vartriangle $ABM = $ displaystyle vartriangle $ ECM suy ra AM = EM. Rồi ứng dụng tính chất đường trung tuyến trong tam giác vuông ADE để suy ra DM = AM.
Bài toán 11 : Cho hình thang ABCD (AB // CD) có AB = a, CD = b. Trên AD lấy hai điểm E, F sao cho AE = EF = FD, trên BC lấy hai điểm M, N sao cho BM = MN = NC. Tính độ dài các đoạn EM, FN theo a và b.
Gợi ý : Dựa vào đường trung bình của hình thang.
Bài toán 12 : Cho BD là đường trung tuyến của tam giác ABC. E là trung điểm của đoạn thẳng AD, F là trung điểm của đoạn thẳng DC, M là trung điểm của cạnh AB, N là trung điểm của cạnh BC. Chứng minh rằng ME // NF.
Gợi ý :
– ME với BD như thế nào? Tại sao?
– NF với BD như thế nào ? Tại sao?
Bài toán 13 : Cho hình thang ABCD (AB //CD, AB < CD). Gọi M, N lần lượt là trung điểm của AD, CD. Gọi I, K là giao điểm của MN với BD và AC.
Chứng minh rằng : IK = $ displaystyle frac{1}{2}$(CD – AB).
Gợi ý :
– Học sinh tự vẽ hình.
– Chứng minh MK là đường trung bình cuả tam giác ACD.
– Chứng minh MI là đường trung bình của tam giác ABD.
– IK = MK – MI.
Bài toán 14 : Cho tam giác ABC. Gọi M là trung điểm của BC. Trên tia đối của tia BA lấy điểm D sao cho BD = AB. Gọi K là giao điểm của DM và AC. Chứng minh rằng AK = 2KC.
Gợi ý :
– Học sinh tự vẽ hình mình họa.
– Gọi N là trung điểm của AK.
– BN là đường trung bình của tam giác ADK suy BN//DK suy ra BN//MK.
– Đi chứng minh MK là đường trung bình của tam giác BNC suy ra K là trung điểm của NC.
– Từ các dữ kiện trên học sinh suy ra AK = 2KC.
