Chuyên đề Hàm số lượng giác lớp 10 bao gồm kiến thức lý thuyết lượng giác cần nhớ và các bài tập tự giải.
A. Kiến thức cần nhớ
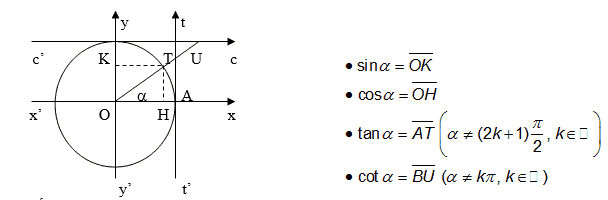
1. Các hằng đẳng thức cơ bản
a) $ {{sin }^{2}}x {{cos }^{2}}x=1$
b) $ tan x=frac{{sin x}}{{cos x}}$
c) $ cot x=frac{{cos x}}{{sin x}}$
d) $ 1 {{tan }^{2}}x=frac{1}{{{{{cos }}^{2}}x}}$
e) $ 1 {{cot }^{2}}x=frac{1}{{{{{sin }}^{2}}x}}$ f) $ tan x.cot x=1$
2. Giá trị của các hàm lượng giác cung liên quan đặc biệt
a) Hai cung đối nhau
$ begin{array}{l}cos (-x)=cos xsin (-x)=-sin xtan (-x)=-tan xcot (-x)=-cot xend{array}$
b) Hai cung bù nhau
$ begin{array}{l}sin (pi -x)=sin xcos (pi -x)=-cos xtan (pi -x)=-tan xcot (pi -x)=-cot xend{array}$
c) Hai cung khác nhau
$ begin{array}{l}sin (x 2pi )=sin xcos (x 2pi )=cos xtan (x 2pi )=tan xcot (x 2pi )=cot xend{array}$
d) Hai cung khác nhau
$ begin{array}{l}sin (pi x)=-sin xcos (pi x)=-cos xtan (pi x)=tan xcot (pi x)=cot xend{array}$
e) Hai cung phụ nhau
$ begin{array}{l}sin left( {frac{pi }{2}-x} right)=cos xtext{ };text{ }cos left( {frac{pi }{2}-x} right)=sin xtan left( {frac{pi }{2}-x} right)=cot xtext{ ; }cot left( {frac{pi }{2}-x} right)=tan xend{array}$
B. Bài tập
1. Tìm các giá trị của $ alpha $để biểu thức sau đạt giá trị nhỏ nhất. Tìm giá trị nhỏ nhất đó.
$ A=frac{1}{{1 sin alpha }}text{ ; }B=frac{1}{{1-cos alpha }}$
2. Xét dấu của các biểu thức sau:
a) $ sin {{123}^{o}}-sin {{132}^{o}}$
b) $ cot {{304}^{o}}-cot {{316}^{o}}$
3. Rút gọn các biểu thức sau:
a) $ 5tan {{540}^{o}} 2cos {{1170}^{o}} 4sin {{990}^{o}}-3cos {{540}^{o}}$
b) $ 3sin frac{{25pi }}{6}-3tan frac{{13pi }}{4} 2cos frac{{19pi }}{3}$
c) $ {{sin }^{2}}{{15}^{o}} {{sin }^{2}}{{35}^{o}} {{sin }^{2}}{{55}^{o}} {{sin }^{2}}{{75}^{o}}$
d) $ {{cos }^{2}}{{15}^{o}} {{cos }^{2}}{{35}^{o}} {{cos }^{2}}{{55}^{o}} {{cos }^{2}}{{75}^{o}}$
e) $ {{sin }^{2}}frac{pi }{{12}} {{sin }^{2}}frac{{3pi }}{{12}} {{sin }^{2}}frac{{5pi }}{{12}} {{sin }^{2}}frac{{7pi }}{{12}} {{sin }^{2}}frac{{9pi }}{{12}} {{sin }^{2}}frac{{11pi }}{{12}}$
f) $ {{cos }^{2}}frac{pi }{{12}} {{cos }^{2}}frac{{3pi }}{{12}} {{cos }^{2}}frac{{5pi }}{{12}} {{cos }^{2}}frac{{7pi }}{{12}} {{cos }^{2}}frac{{9pi }}{{12}} {{cos }^{2}}frac{{11pi }}{{12}}$
g) $ sin (pi a)-cos left( {frac{pi }{2} a} right) cot (2pi -a) tan left( {frac{{3pi }}{2} a} right)$
h) $ A={{sin }^{4}}a {{cos }^{2}}a {{sin }^{2}}a.{{cos }^{2}}a$
i) $ B=frac{{{{{left( {sin frac{a}{2} cos frac{a}{2}} right)}}^{2}}-1}}{{tan frac{a}{2}-sin frac{a}{2}.cos frac{a}{2}}}$
j) $ C=frac{{{{{cos }}^{2}}{{{696}}^{o}} tan (-{{{260}}^{o}}).tan {{{530}}^{o}}-{{{cos }}^{2}}156}}{{{{{tan }}^{2}}{{{252}}^{o}} {{{cot }}^{2}}{{{342}}^{o}}}}$
k) $ {{left[ {tan frac{{17pi }}{4} tan left( {frac{{7pi }}{2}-b} right)} right]}^{2}} {{left[ {cot frac{{13pi }}{4} cot left( {7pi -b} right)} right]}^{2}}$
l) $ left( {sqrt{{frac{{1-sin x}}{{1 sin x}}}}-sqrt{{frac{{1 sin x}}{{1-sin x}}}}} right)left( {sqrt{{frac{{1-cos x}}{{1 cos x}}}}-sqrt{{frac{{1 cos x}}{{1-cos x}}}}} right)$
m) $ {{sin }^{3}}a(1 cot a) {{cos }^{3}}a(1 tan a)$
n) $ frac{{tan b}}{{tan b cot b}}$
o) $ frac{{1-{{{cos }}^{4}}a-{{{sin }}^{4}}a}}{{{{{cos }}^{4}}a}}$
p) $ frac{{sin (x-pi ).cos (x-2pi ).sin (2pi -x)}}{{sin left( {frac{pi }{2}-x} right).cot (pi -x).cot left( {frac{{3pi }}{2} x} right)}}$
q) $ {{left[ {sin left( {frac{pi }{2}-x} right) sin (pi -x)} right]}^{2}} {{left[ {cos left( {frac{{3pi }}{2}-x} right) cos (2pi -x)} right]}^{2}}$
r) $ sin left( {frac{pi }{3}-a} right).tan left( {frac{{2pi }}{3} a} right).cos left( {frac{{5pi }}{3} a} right) tan (pi a).tan left( {frac{{3pi }}{2}-a} right)$
s) $ frac{{cot (5,5pi -a) tan (b-4pi )}}{{cot (a-6pi )-tan (b-3,5pi )}}$
t) $ tan {{50}^{o}}.tan {{190}^{o}}.tan {{250}^{o}}.tan {{260}^{o}}.tan {{400}^{o}}.tan {{700}^{o}}$
4. Cho A, B, C là ba góc của tam giác ABC. Chứng minh:
a) $ sin (A B)=sin Ctext{; cos(B} text{C)}=text{-cosA}$ c) $ tan (A C)=-tan B;text{ cot(A} text{B)}=text{-cotC}$
b) $ text{sin}frac{{text{A} text{B}}}{text{2}}=cos frac{C}{2}text{; cos}frac{{text{B} text{C}}}{text{2}}=sin frac{A}{2}$ d) $ tan frac{{A C}}{2}=cot frac{B}{2};text{ cot}frac{{text{A} text{B}}}{text{2}}=tan frac{C}{2}$
5. Tìm giá trị lớn nhất của hàm số: $ y=frac{{2 cos x}}{{sin x cos x-2}}$
6. Tìm giá trị nhỏ nhất và lớn nhất của hàm số trong khoảng $ -pi
