Đề khảo sát chất lượng đầu năm học môn Toán lớp 7 thị xã Chí Linh, tỉnh Hải Dương năm học 2018-2019. Thời gian làm bài: 60 phút. Có đáp án.
Câu 1 (2,5 điểm). Thực hiện phép tính (Tính nhanh nếu có thể):
| a) $ 3frac{1}{4}+(-5).frac{1}{5}-left( {-7frac{3}{4}} right)$ | b) $ -frac{1}{2}-left( {frac{{-3}}{5}} right)+left( {frac{{-1}}{9}} right)+frac{1}{{27}}+frac{7}{{18}}+frac{4}{{35}}-left( {-frac{2}{7}} right)$ |
| c) $ frac{{frac{4}{{17}}-frac{4}{{49}}+frac{4}{{31}}}}{{frac{3}{{17}}-frac{3}{{49}}+frac{3}{{31}}}}$ | |
Câu 2 (2,5 điểm). Tìm x, biết
| a) $ 3-x=1frac{1}{4}$ | b) $ x-35%x=frac{{13}}{2}$ | c) $ 3frac{1}{3}x+16frac{3}{4}=1,75$ |
Câu 3 (2,0 điểm).
Một lớp học có 45 học sinh bao gồm học sinh Giỏi, Khá và Trung bình. Số học sinh Trung bình chiếm $ frac{7}{{15}}$ số học sinh cả lớp. Số học sinh khá bằng $ frac{5}{8}$ số học sinh còn lại. Tính số học sinh Giỏi của lớp.
Câu 4 (2,0 điểm).
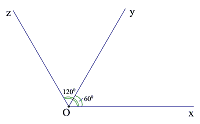
Trên cùng một nửa mặt phẳng có bờ chứa tia Ox, vẽ hai tia Oy, Oz sao cho $ widehat{{xOy}}={{60}^{0}}$ và $ widehat{{xOz}}={{120}^{0}}$.
a) Tính $ widehat{{ytext{O}z}}$.
b) Tia Oy có là tia phân giác của $ widehat{{xtext{O}z}}$ không? Vì sao?
Câu 5 (1,0 điểm).
So sánh A và B biết: $ A=frac{{{{7}^{{2013}}}+1}}{{{{7}^{{2014}}}+1}}$ và $ B=frac{{{{7}^{{2014}}}+1}}{{{{7}^{{2015}}}+1}}$.
HƯỚNG DẪN CHẤM KHẢO SÁT CHẤT LƯỢNG ĐẦU NĂM MÔN TOÁN 7
| Câu | Đáp án | Điểm |
| 1
(2,5 đ) |
a) $ 3frac{1}{4}+(-5).frac{1}{5}-left( {-7frac{3}{4}} right)=3frac{1}{4}-1+7frac{3}{4}=10$ | 1,0 |
| b) $ -frac{1}{2}-left( {frac{{-3}}{5}} right)+left( {frac{{-1}}{9}} right)+frac{1}{{27}}+frac{7}{{18}}+frac{4}{{35}}-left( {-frac{2}{7}} right)$
$ =left[ {-frac{1}{2}+left( {frac{{-1}}{9}} right)+frac{7}{{18}}} right]+left[ {frac{3}{5}+frac{4}{{35}}+frac{2}{7}} right]+frac{1}{{27}}$$ =frac{{-2}}{9}+1+frac{1}{{27}}=frac{{22}}{{27}}$ |
0,75 | |
| c) $ frac{{frac{4}{{17}}-frac{4}{{49}}+frac{4}{{31}}}}{{frac{3}{{17}}-frac{3}{{49}}+frac{3}{{31}}}}=frac{{4left( {frac{1}{{17}}-frac{1}{{49}}+frac{1}{{31}}} right)}}{{3left( {frac{1}{{17}}-frac{1}{{49}}+frac{1}{{31}}} right)}}=frac{4}{3}$ | 0,75 | |
| 2
(2,5 đ) |
a) $ x=frac{7}{4}$ | 1,0 |
| b) $ x=10$ | 0,75 | |
| c) $ x=-frac{9}{2}$ | 0,75 | |
| 3
(2,0 đ) |
Số học sinh trung bình của lớp là: $ frac{7}{{15}}.45=21$(học sinh) | 1 |
| Số học sinh khá của lớp là: $ frac{5}{8}.(45-21)=15$ (học sinh) | 0,5 | |
| Số học sinh giỏi của lớp là: $ 45-(21+15)=9$ (học sinh) | 0,5 | |
| 4
(2,0 đ) |
Vẽ hình đúng:
|
0,5 |
| a) Trên cùng một nửa mặt phẳng có bờ chứa tia Ox có:
$ widehat{{xOy}}={{60}^{0}}<widehat{{xOz}}={{120}^{0}}$ nên tia Oy nằm giữa hai tia Ox và Oz. Do đó: $ begin{array}{l}widehat{{xOy}}+widehat{{yOz}}=widehat{{xOz}}{{60}^{0}}text{ + }widehat{{yOz}}={{120}^{0}}text{ }widehat{{yOz}}={{60}^{0}}end{array}$ |
1,0 | |
| b) Tia Oy là tia phân giác của góc xOz vì:
– Tia Oy nằm giữa hai tia Ox và Oz – $ widehat{{xOy}}=widehat{{yOz}}={{60}^{0}}$ |
0,5 | |
| 5
(1,0 đ) |
Ta có:
$ displaystyle 7A=frac{{7left( {{{7}^{{2013}}}+1} right)}}{{{{7}^{{2014}}}+1}}=frac{{{{7}^{{2014}}}+7}}{{{{7}^{{2014}}}+1}}=frac{{{{7}^{{2014}}}+1+6}}{{{{7}^{{2014}}}+1}}=1+frac{6}{{{{7}^{{2014}}}+1}}$ $ displaystyle 7B=frac{{7left( {{{7}^{{2014}}}+1} right)}}{{{{7}^{{2015}}}+1}}=frac{{{{7}^{{2015}}}+7}}{{{{7}^{{2015}}}+1}}=frac{{{{7}^{{2015}}}+1+6}}{{{{7}^{{2015}}}+1}}=1+frac{6}{{{{7}^{{2015}}}+1}}$ |
0,5 |
| Vì $ displaystyle frac{6}{{{{7}^{{2014}}}+1}}>frac{6}{{{{7}^{{2015}}}+1}}$ nên $ 7text{A}>7B$ hay $ A>B$ | 0,5 |