BÀI TẬP TUẦN 1
– Căn thức bậc hai $ displaystyle sqrt{{{A}^{2}}}=left| A right|$
– 1 số hệ thức cạnh và đường cao trong tam giác vuông
Bài 1: So sánh
a) 5 và $ displaystyle sqrt{26}$
b) $ displaystyle -sqrt{26}$ và $ displaystyle -sqrt{29}$
c) $ displaystyle sqrt{37}+sqrt{10}$ và $ displaystyle sqrt{80}$
Bài 2: Tính giá trị biểu thức:
a) $ displaystyle sqrt{frac{25}{49}}-sqrt{frac{1}{16}}+sqrt{{{(-2)}^{2}}}$
b) $ displaystyle {{left( sqrt{3} right)}^{2}}sqrt{0,25}-0,2sqrt{{{left( -3 right)}^{2}}}$
c) $ displaystyle sqrt{{{113}^{2}}-{{112}^{2}}}$
d) $ displaystyle sqrt{{{left( -0,1 right)}^{4}}}+sqrt{{{58}^{2}}-{{42}^{2}}}$
e) $ displaystyle sqrt{{{left( sqrt{10}-3 right)}^{2}}}+sqrt{{{left( sqrt{10}-4 right)}^{2}}}$
f) $ displaystyle sqrt{11+6sqrt{2}}+sqrt{11-6sqrt{2}}$
g)$ displaystyle sqrt{29+12sqrt{5}}+sqrt{29-12sqrt{5}}$
Bài 3: Tìm x để biểu thức sau có nghĩa
a) $ displaystyle sqrt{3x-1}$
b) $ displaystyle sqrt{frac{2}{x-1}}$
c) $ displaystyle sqrt{5+{{x}^{2}}}$
d)$ displaystyle sqrt{frac{x-1}{2x-4}}$
Bài 4: Tìm x, biết:
a) $ displaystyle sqrt{{{x}^{2}}}=left| -7 right|$
b) $ displaystyle frac{sqrt{9-4sqrt{5}}}{2-sqrt{5}}$$ displaystyle sqrt{36{{x}^{2}}}=10$
c) $ displaystyle sqrt{4{{x}^{2}}-4x+1}=5$
d) $ displaystyle sqrt{{{x}^{2}}-4x+25}=5$
e) $ displaystyle sqrt{x}<2$
f) $ displaystyle frac{4-2sqrt{x}}{sqrt{x}+1}>0$
g*) $ displaystyle sqrt{x+4sqrt{x-4}}=2$
h*) $ displaystyle sqrt{2x-2+2sqrt{2x-3}}+sqrt{2x+13+8sqrt{2x-3}}=5$
Bài 5: Phân tích đa thức thành nhân tử, rút gọn biểu thức:
a) x2 – 10
b) $ displaystyle x-4sqrt{x}+4$
c) $ displaystyle frac{x-6sqrt{x}+9}{x-9}$
d) $ displaystyle frac{sqrt{9-4sqrt{5}}}{2-sqrt{5}}$
e*) $ displaystyle frac{sqrt{9+2sqrt{2}+2sqrt{3}+2sqrt{2}sqrt{3}}}{6+3sqrt{2}+3sqrt{3}}$
Bài 6*: Tìm x,y,z biết: $ displaystyle frac{x+y+z}{2}-3020=sqrt{x-2017}+2sqrt{y-2018}+3sqrt{z-2019}$
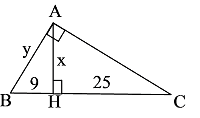
Bài 7: Tìm x, y có trên hình vẽ sau :
Bài 8: Cho tam giác ABC, đường cao AH, biết AB2 = BH.BC. Chứng minh tam giác ABC vuông.
Bài 9: Cho ΔABC vuông tại A, đường cao AH. Biết HB = 3,6cm ; HC = 6,4cm
a)Tính độ dài các đoạn thẳng: AB, AC, AH.
b) Kẻ HE$ displaystyle bot $AB ; HF$ displaystyle bot $AC. Chứng minh rằng: AB.AE = AC.AF
Bài 10: Cho tam giác ABC vuông ở A, phân giác AD, đường cao AH. Biết CD = 68cm, BD = 51cm. Tính BH, HC.
Bài 11: Cho hình thang ABCD có $ displaystyle widehat{B}text{ = }widehat{text{C}}text{ = 9}{{text{0}}^{text{o}}}$, hai đường chéo vuông góc với nhau tại H. Biết rằng AB = $ displaystyle 3sqrt{5}$cm; HA = 3cm. Chứng minh rằng:
a) HA : HB : HC : HD = 1 : 2 : 4 : 8
b) $ displaystyle frac{text{1}}{text{A}{{text{B}}^{text{2}}}}-frac{text{1}}{text{C}{{text{D}}^{text{2}}}}=frac{text{1}}{text{H}{{text{B}}^{text{2}}}}-frac{text{1}}{text{H}{{text{C}}^{text{2}}}}$
