Đề cương ôn tập học kì 1 môn Toán lớp 8, trường THCS Mai Dịch, quận Cầu Giấy, TP Hà Nội, năm học 2019-2020.
Có lý thuyết, ôn tập 2 phần Đại số và Hình học.
I. TRỌNG TÂM
1. Kiến thức:
Kiến thức cơ bản
Đại số
– Học sinh nẵm vững kiến thức cơ bản về: Các phép tính về đa thức, phân thức.
Hình học
– Nắm vững định nghĩa, tính chất, dấu hiệu nhận biết tứ giác đặc biệt, đường trung bình của tam giác, hình thang. Áp dụng các công thức tính diện tích trong các bài tập tính toán.
Nâng cao
– Giá trị nhỏ nhất, lớn nhất của biểu thức dạng phân thức, đa thức.
– Biến đổi biểu thức.
2. Kỹ năng:
Vẽ hình, chứng minh,…..
PHẦN ĐẠI SỐ
DẠNG I: PHÂN TÍCH ĐA THỨC THÀNH NHÂN TỬ
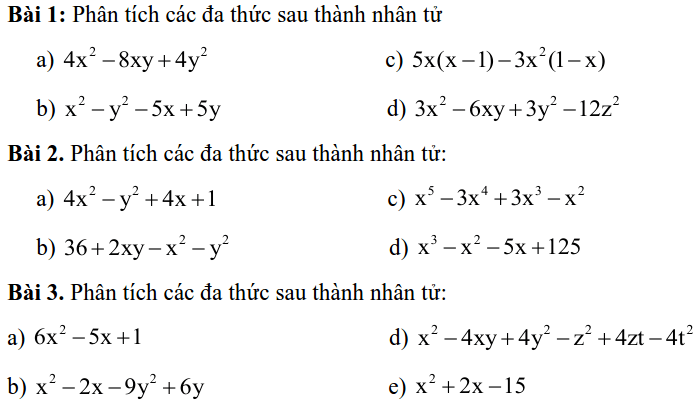
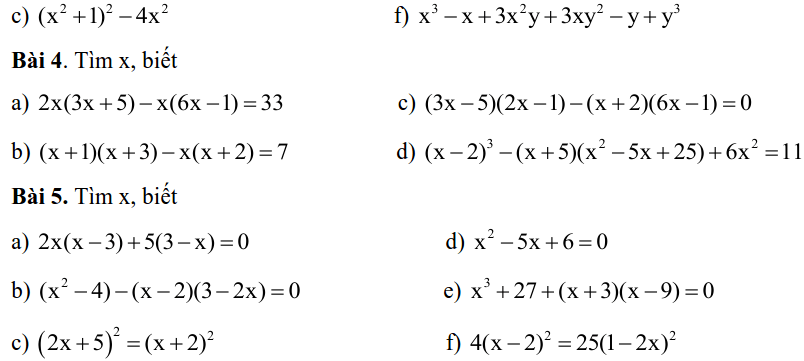
DẠNG 2: TÍNH GIÁ TRỊ BIỂU THỨC
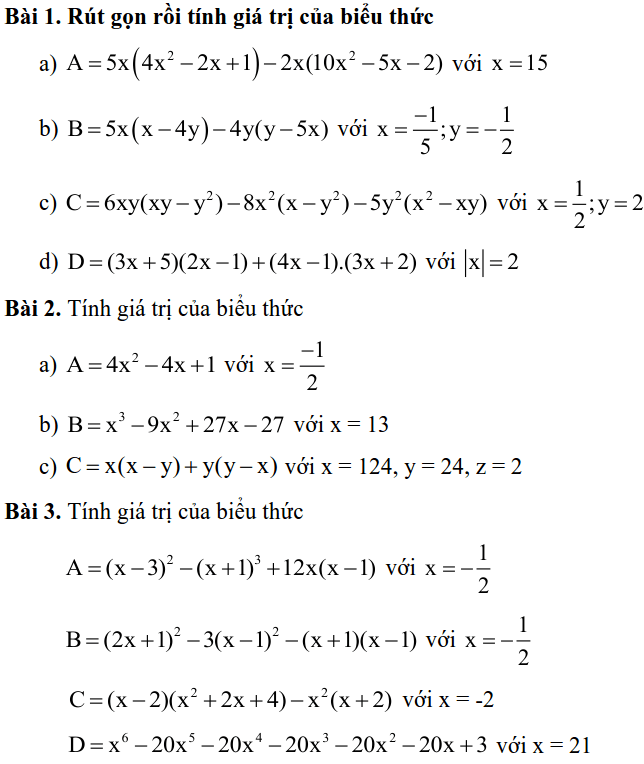
DẠNG 3: CHIA ĐA THỨC

DẠNG 4: CÁC PHÉP TÍNH VỀ PHÂN THỨC

DẠNG 5: NÂNG CAO

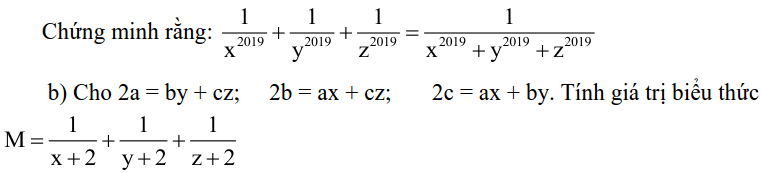
PHẦN HÌNH HỌC
Bài 1: Cho $ Delta ABC$có 3 góc nhọn AB < AC. Các đường cao BE, CF cắt nhau tại H. Gọi M là trung điểm của BC. K là điểm đối xứng với H qua M.
a) Chứng minh: Tứ giác BHCK là hình bình hành.
b) Chứng minh: $ BKbot AB$ và $ CKbot AC$
c) Gọi I là điểm đối xứng với H qua BC. Chứng minh: Tứ giác BIKC là hình thang cân.
d) BK cắt HI tại G. Tam giác ABC phải có thêm điều kiện gì để tứ giác GHCK là hình thang cân.
Bài 2: Cho tam giác ABC cân tại A, đường cao AD, O là trung điểm AC, điểm E đối xứng với điểm D qua điểm O.
a) Chứng minh tứ giác AECD là hình chữ nhật
b) Gọi I là trung điểm của AD, chứng tỏ I là trung điểm của BE
c) Cho AB = 10cm, BC = 12cm, tính diện tích tam giác OAD.
d) Đường thẳng OI cắt AB tại K. Tìm điều kiện của tam giác ABC để tứ giác AEDK là hình thang cân.
Bài 3: Cho $ Delta ABC$đều, D, E, F lần lượt là trung điểm của AB, AC, BC. Trên tia đối của tia ED lấy điểm M sao cho DE = EM, DF cắt CM tại N.
a) Chứng minh rằng BDEF là hình thoi?
b) Chứng minh rằng ADCM là hình chữ nhật
c) Chứng minh $ Delta FMN$ vuông
d) Gọi P là giao điểm BE và DF, Q là giao điểm của EC và FM. Chứng minh EF, DC, BM, PQ đồng quy.
Bài 4: Cho $ Delta ABC$vuông tại A, (AB < AC). Gọi M, N, E lần lượt là trung điểm của AB, AC, BC.
a) Chứng minh: Tứ giác ANEB là hình thang vuông
b) Chứng minh: Tứ giác AMEN là hình chữ nhật.
c) Gọi D là điểm đối xứng của E qua M . Chứng minh: Tứ giác BEAD là hình thoi.
d) Tam giác ABC cần có thêm điều kiện gì để tứ giác AMEN là hình vuông?
Bài 5. Cho $ Delta ABC$nhọn (AB < AC). Kẻ đường cao AH. Gọi M là trung điểm của AB, N là điểm đối xứng của H qua M.
a) Chứng minh: Tứ giác ANBH là hình chữ nhật.
b) Trên tia đối của tia HB lấy điểm E sao cho H là trung điểm của BE. Gọi F là điểm đối xứng với A qua H. Tứ giác ANHE là hình gì? Vì sao?
c) Gọi I là giao điểm của AH và NE. Chứng minh: MI//BC
d) Đường thẳng MI cắt AC tại K. Kẻ $ NQbot KH$ tại Q. Chứng minh: $ AQbot BQ$
