Đề khảo sát chất lượng đầu năm môn Toán lớp 8 thành phố Ninh Bình, năm học 2018-2019. Có đáp án.
Thời gian làm bài: 90 phút
Phần I – Trắc nghiệm (2,0 điểm)
Hãy viết chữ cái in hoa đứng trước phương án đúng trong mỗi câu sau vào bài làm.
Câu 1: Kết quả của phép nhân x.(x+3) là :
| A. x2 + 3x | B. x2 + 3 | C. 3x + 3 | D. 3x2 |
Câu 2: Kết quả của phép nhân 3xy.(4x2 – y) là :
| A. 12x3y – y | B. 12x3y -xy2 | C.12x3y +3xy2 | D. 12x3y – 3xy2 |
Câu 3: Cho y = f(x) = (2x+3)(3x-4) thì giá trị của f($ displaystyle frac{1}{2}$) là:
| A. -10 | B. -2 | C. $ displaystyle -frac{{25}}{4}$ | D. Kết quả khác |
Câu 4: Trong mặt phẳng, khẳng định nào sau đây là đúng:
| A. Tứ giác có 4 góc tù. | B. Tứ giác có 4 góc vuông. |
| C. Tứ giác có 4 góc nhọn. | D. Tứ giác có 2 góc nhọn và 2 góc vuông. |
Phần II – Tự luận (8,0 điểm)
Câu 5 (2,5 điểm)
1) Cho đơn thức$ displaystyle text{A}=left( {text{-}frac{text{3}}{text{4}}{{text{x}}^{text{2}}}{{text{y}}^{4}}{{text{z}}^{text{3}}}} right)left( {frac{text{8}}{text{3}}{{text{x}}^{text{3}}}{{text{y}}^{text{5}}}{{text{z}}^{text{4}}}} right)$. Thu gọn đơn thức A. Xác định phần hệ số và tìm bậc của đơn thức thu gọn.
Cho biểu thức $ displaystyle text{B},,text{=},text{3}{{text{x}}^{text{2}}}text{y},text{-},text{xy},text{+},text{6}$. Tính giá trị của B tại $ text{x}=2,,,left| text{y} right|=1$
Câu 6 (2,0 điểm)
1) Cho hai đa thức: $ displaystyle text{M}left( text{x} right)text{=3}{{text{x}}^{text{4}}}text{-},text{2}{{text{x}}^{text{3}}}text{+},{{text{x}}^{text{2}}}text{+},text{4x},text{-},text{5}$ và $ displaystyle text{N}left( text{x} right)text{=},text{2}{{text{x}}^{text{3}}}text{+},{{text{x}}^{text{2}}}text{-},text{4x},text{-},text{5}$.
a) Tính $ displaystyle text{M(x)},text{+},text{N(x)}$.
b) Tìm đa thức P(x) biết: P(x) + N(x) = M(x).
2) Tìm nghiệm của các đa thức sau:
a) $ text{x},text{-},text{2}$.
b) $ text{(}{{text{x}}^{text{2}}}text{+},text{2)(}{{text{x}}^{text{2}}}text{-},text{9)}$ .
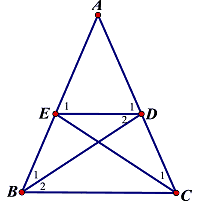
Câu 7 (3,0 điểm) Cho $ displaystyle text{ }!!Delta!!text{ ABC}$cân tại A. Tia phân giác của $ displaystyle widehat{{ABC}}$ cắt AC tại D, tia phân giác của $ displaystyle widehat{{ACB}}$ cắt AB tại E. Chứng minh rằng:
a) $ displaystyle text{ }!!Delta!!text{ ABD}$=$ displaystyle text{ }!!Delta!!text{ ACE}$.
b) $ text{DE//BC}$.
c) $ text{BE},text{=},text{ED},text{=},text{DC}$.
Câu 8 (0,5 điểm) Cho 20 điểm phân biệt trong mặt phẳng, trong đó có n điểm thẳng hàng. Cứ qua 2 điểm trong 20 điểm đã cho, ta vẽ một đường thẳng. Tìm n, nếu vẽ được tất cả là 170 đường thẳng.
HƯỚNG DẪN CHẤM ĐỀ KHẢO SÁT CHẤT LƯỢNG ĐẦU NĂM MÔN TOÁN 8:
| Câu | Đáp án | Điểm |
| Phần I – Trắc nghiệm (2,0 điểm). Mỗi câu trả lời đúng được 0,5 điểm. | ||
|
||
| Phần II – Tự luận (8,0 điểm) | ||
| 5
(2,5 điểm) |
1) $ displaystyle text{A}=left( {text{-}frac{text{3}}{text{4}}{{text{x}}^{text{2}}}{{text{y}}^{4}}{{text{z}}^{text{3}}}} right)left( {frac{text{8}}{text{3}}{{text{x}}^{text{3}}}{{text{y}}^{text{5}}}{{text{z}}^{text{4}}}} right),=,-2{{text{x}}^{5}}{{text{y}}^{9}}{{text{z}}^{7}}$ | 0,50 |
| Hệ số của A là: -2 | 0,25 | |
| Bậc của A là : 5 + 9 + 7 = 21 | 0,5 | |
| 2) Ta có: $ left| y right|=1Rightarrow left[ begin{array}{l}y=1y=-1end{array} right.$ | 0,25 | |
| Thay x = 2; y = 1 vào biểu thức $ displaystyle B=3{{x}^{2}}y-xy+6$ ta được: $ displaystyle B={{3.2}^{2}}.1-2.1+6=16$ | 0,5 | |
| Thay x = 2; y = -1 vào biểu thức $ displaystyle B=3{{x}^{2}}y-xy+6$ được:$ displaystyle B={{3.2}^{2}}.(-1)-2.(-1)+6=-4$ | 0,5 | |
| 6
(2,0 điểm) |
1) (1,0 điểm) | |
| a)Từ $ displaystyle text{M}left( text{x} right)text{=3}{{text{x}}^{text{4}}}text{-},text{2}{{text{x}}^{text{3}}}text{+},{{text{x}}^{text{2}}}text{+},text{4x},text{-},text{5}$ ; $ displaystyle text{N}left( text{x} right)text{=},text{2}{{text{x}}^{text{3}}}text{+},{{text{x}}^{text{2}}}text{-},text{4x},text{-},text{5}$nên
$ displaystyle text{M(x)},text{+},text{N(x)}$=$ displaystyle text{=3}{{text{x}}^{text{4}}}text{+},2{{text{x}}^{text{2}}},text{-},10$ |
0,5 | |
| b)Từ: P(x) + N(x) = M(x) $ Rightarrow $ $ displaystyle text{P}left( text{x} right)text{=M}left( text{x} right)text{-N}left( text{x} right)text{=3}{{text{x}}^{text{4}}}text{-},text{4}{{text{x}}^{text{3}}}text{+},text{8x}$ | 0,5 | |
| 2) (1,0 điểm) | ||
| a)Tìm dược nghiệm của đa thức x-2 là x=2 | 0,5 | |
| b)Tìm được nghiệm của đa thức $ text{(}{{text{x}}^{text{2}}}text{+},text{2)(}{{text{x}}^{text{2}}}text{-},text{9)}$ là $ text{x},text{=},pm text{3}$ | 0,5 | |
| 7
(3,0 điểm) |
Vẽ hình đúng để làm được ý a: 0,25 điểm
|
0,25 |
| 1) $ displaystyle Delta ABC$cân tại $ Rightarrow AB=AC;widehat{{ABC}}=widehat{{ACB}}$ | 0,25 | |
| BD là phân giác của $ displaystyle widehat{{ABC}},,(gt)Rightarrow {{widehat{B}}_{1}}=frac{1}{2}widehat{{ABC}}$; CE là phân giác của $ displaystyle widehat{{ACB}},,(gt)Rightarrow {{widehat{C}}_{1}}=frac{1}{2}widehat{{ACB}}$. Do đó $ displaystyle {{widehat{B}}_{1}}={{widehat{C}}_{1}}$ | 0,25 | |
| Do đó $ displaystyle Delta ABD$=$ displaystyle Delta ACE$ (g.c.g) | 0,25 | |
| 2)$ displaystyle Delta ABD$=$ displaystyle Delta ACE$ (g.c.g) $ Rightarrow AD=AE$ (hai cạnh tương ứng) | 0,25 | |
| $ Rightarrow $ $ displaystyle Delta ADE$cân tại $ A$ $ Rightarrow $ $ displaystyle {{widehat{E}}_{1}}=frac{{{{{180}}^{0}}-widehat{A}}}{2}$ | 0,25 | |
| $ displaystyle Delta ABC$cân tại $ A$ $ Rightarrow $$ displaystyle widehat{{ABC}}=frac{{{{{180}}^{0}}-widehat{A}}}{2}$ | 0,25 | |
| Do đó $ displaystyle {{widehat{E}}_{1}}=widehat{{ABC}}Rightarrow DE//BC$(hai góc đồng vị bằng nhau) | 0,25 | |
| 3)Ta có $ displaystyle DE//BC$(chứng minh trên)$ Rightarrow {{widehat{B}}_{2}}={{widehat{D}}_{2}}$ ( hai góc so le trong)
mà $ displaystyle {{widehat{B}}_{1}}={{widehat{B}}_{2}}$(gt) nên $ displaystyle {{widehat{B}}_{1}}=widehat{{{{D}_{2}}}}$ $ Rightarrow $ $ displaystyle Delta EBD$cân tại E $ Rightarrow EB=ED$ |
0,25 | |
| Chứng minh tương tự ta cũng có $ DC=ED$ | 0,25 | |
| Do đó $ BE=ED=DC$(đpcm) | 0,25 | |
| 8
(0,5 điểm) |
Nếu trong 20 điểm, không có 3 điểm nào thẳng hàng thì số đường thẳng vẽ được là:$ frac{{19.20}}{2}=190$. Trong n điểm, nếu không có 3 điểm nào thẳng hàng thì số đường thẳng vẽ được là: $ displaystyle frac{{n(n-1)}}{2}$. Thực tế, qua n điểm này ta chỉ vẽ được 1 đường thẳng nên tổng số đường thẳng vẽ được là: $ displaystyle 190-frac{{n(n-1)}}{2}+1$ | 0,25
|
| Theo đề bài ta có: $ displaystyle 190-frac{{n(n-1)}}{2}+1=170$. Tìm được n = 7 | 0,25 | |