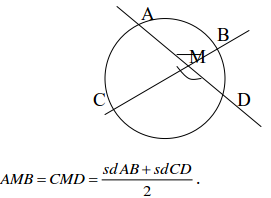
1. Cho (O) và M trong (O) khi đó có hai đường thẳng cùng qua M tạo thành góc. Góc này là góc bên trong đường tròn. Hai đường thẳng này cắt đường tròn tạo thành các cung.
2. Khi đó số đo góc ở trong đường tròn bằng tổng số đo hai cung này chia hai.
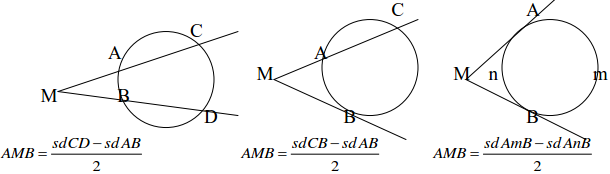
3. Cho (O) và M ngoài (O) khi đó góc mà các cạnh của nó luôn tiếp xúc hoặc cắt (O) gọi là góc ngoài đường tròn (O) tại M. Khi đó góc này cũng cắt đường tròn tao thành hai cung; một cung lớn và một cung nhỏ.
4. Số đo góc ngoài bằng sđ cung lớn – cung nhỏ sau đó chia hai.
Bài tập:
1. Cho 4 điểm A; B; C và D theo thứ tự trên (O) sao cho: số đo các cung như sau: AB= 400; CD=1200. Gọi I là giao điểm AC và biến đổi. M là giao điểm của DA và CB kéo dài. Tính các góc CID và AMB.
2. Cho (O); từ M ngoài (O) ta vẽ cát tuyến MAC và MBD sao cho góc CMD có số đo 400. Gọi E là giao điểm của AD và BC. Biết góc AEB là 700; tính số đo các cung AB và CD.
3. Cho (O) và M ngoài (O); vẽ tiếp tuyến MA và cát tuyến MBC đi qua O (B nằm giữa M và C). Đường tròn đường kính MB gặp MA tại E.
C/m: sd AnC = sdBmA + sdBkE với AnC; BmA và BkE là các cung trong góc AMC.
